ex和dx的关系

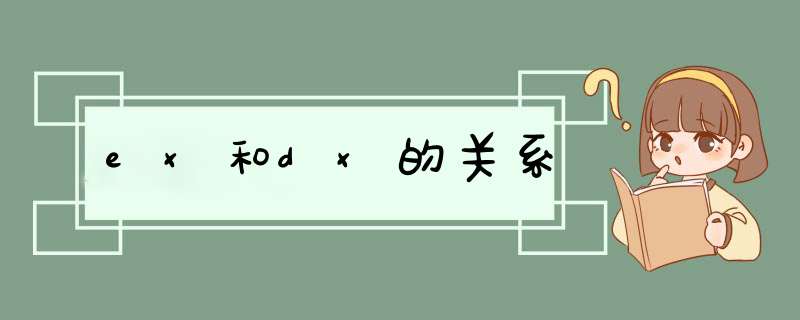
D（X）指方差，E（X）指期望，关系为：DX＝E（X－E（X））＾2＝E｛X＾2－2XE（X）＋（E（X））＾2｝＝E（X＾2）2（E（X））＾2＋（E（X））＾2。

方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。

在概率论和统计学中，数学期望（或均值，也简称期望）是最基本的数学特征之一，它是一个实验中每个可能结果的概率乘以结果的总和。它反映了随机变量的平均值。

扩展资料：

对于连续随机变量X，若定义域为（a，b），概率密度函数为F（X），则连续随机变量X的方差计算公式为：D（X）＝（X－）＾2f（X）dx。方篆差描述了随机变量的值与其数学期望的离散程度（标准差和方差越大，离散程度越大）。

如果X值集中，D（X）的方差较小；如果X的值是分散的，那么D（X）的方差就很大。

所以D（X）是对X离散程度的度量，它是对X离散程度的度量。