PRC-CW雷达地杂波相关特性分析

PRC-CW雷达地杂波相关特性分析

本文分析了在低俯视角情形时地杂波要引起雷达回波信号展宽的事实，对于伪码调相连续波雷达来讲，某一时刻的回波信号将是此前一段时间内展宽的回波在此时刻的迭加，提出了计算伪码调相连续波雷达回波信号的迭加方法，在以往对地杂波特性研究结果的基础上，同时考虑不同分辨单元间在空间和时间上的相关性质，研究该体制雷达地杂波回波信号的时间相关特性，并进行了计算机模拟，结果表明，与脉冲雷达相比，其地杂波的时间相关性将增强.
　　关键词:伪码调相连续波雷达；地杂波；相关特性

CorrelaTIon CharacterisTIcs Analysis of Land Clutter for PRC-CW Radar

CAO Zhi-guo　ZHANG Zhi-yong
(InsTItute for Pattern RecogniTIon and AI,HUST,Wuhan 430074,China)
ZHANG Tian-xu
(State Key Lab.for Image Processing and Intelligent Control,Wuhan 430074,China)
YUAN Ting　WANG Ke-yu
(Shanghai Electronic Communication Equipment Institute,Shanghai 200081,China)

　　Abstract:It is pointed out that the land clutter,when the radar grazing angle is low,will cause the time spread of radar echo signal,For the pseudo-random code continuous wave (PRC-CW) radar,the echo signal at a specified moment will be the superposition of some spread echo signals in a period of time before this specified moment.A superposition algorithm was proposed to calculated the PRC-CW radar signal.Based on the former results on the characteristics of land clutter,and considering temporal and spatial correlation characteristics between defferent resolution cells,the temporal correlation characteristics of the echo signal of land clutter for the PRC-CW radar are investigated with simulation method.The results indicate that the echo signal of land clutter for PRC-CW radar is more correlated than that for pulse radar.
　　Key words:PRC-CW radar;land clutter;correlation characteristics

一、引　　言
　　随着现代微波固态器件的发展，使得具有较低截获概率、在杂波环境下具有良好的检测能力和有利于反隐身的伪码调相连续波(PRC-CW)雷达，在目标检测、跟踪、制导等方面的实际应用成为可能［1］.但PRC-CW雷达发射的是一种连续波形，因此，在远距离，低俯视角情况下，雷达波照射到地物表面上时，码元回波要产生重叠，其地杂波特性与脉冲雷达体制下的将有所不同.虽然，文献［2］在研究脉冲雷达对于粗糙表面的电磁波散射特性时，应用回波叠加的模型来研究地杂波的概率密度分布特性，但是，它的前提是认为各叠加矢量之间是相互独立的，这与PRC-CW雷达的工作情形不一样，因为PRC-CW雷达各码元回波之间显然是有一定的相关性的，所以，不能够直接应用脉冲雷达体制下地杂波特性的研究结果.为了在设计和使用PRC-CW雷达时，最大限度地发挥其作战效能，必须针对其特殊性来研究目标特性和环境特性，但是，这方面的研究与测试结果在国内外却尚未见公开报道，因此，本文通过理论建模和计算机模拟的方法，来研究PRC-CW雷达的地杂波相关特性.

二、地杂波信号模型及其模拟
　　图1中R为探测距离，θφ为天线垂直波束宽度，φ为波束俯角，τ0为波束前沿与后沿的时差，若τe=(2Rθφctgφ)/c为一个码元回波的时间长度，则当τe＞τ0时，码元回波展宽，回波信号的码元之间会产生重叠，迭加的个数为Q，Q=［τe/τ0］,“［.］”表示上取整，即某一时刻的回波信号将是此前一段时间内Q个展宽的回波在此时刻的迭加.这样，可以把整个雷达波束分成Q个子波束，见图2，每个子波束对地面的距离与俯视角分别为Rq和φq.θq为第q个子波束回波信号的相位，它在(0，2π)间服从均匀分布.Aq是第q个子波束回波信号的幅度，则实际雷达接收到的每个码元信号复振幅是Q个码元回波信号空间矢量迭加的结果：

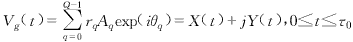　(1)

式中，Vg(t)为实际接收的码元信号复包络，X(t)、Y(t)分别为Vg(t)的同相分量和正交分量，rq为权因子，根据图2所示的雷达波束几何模型，得：

rq=(R0/Rq)3/2cos1/2φ0/cos1/2φq　(2)

式中，R0和φ0为第一个子波束对地面的距离和俯视角.

　　　　　　　　　　　　　　　　　　

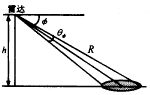
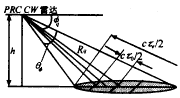
图1　雷达波束示意图

图2　PRC-CW雷达波束示意图

　　若只考虑地杂波雷达散射截面的影响，则Aq=(2σ)1/2,σ为地面分布杂波的雷达散射截面.
　　从图2还可看出，各子波束的回波幅度分别是各分辨单元的后向散射幅度，从空间上看代表了相邻各分辨单元的散射截面的大小，即地杂波的空间分布特性，在一般地物情况下，测试研究表明［3］，地杂波散射系数空间分布的概率密度函数为Weibull分布函数，且其相关性包含了快起伏和慢起伏双尺度的变化，因此，地杂波的归一化空间相关函数为：

R(d)=asexp(-d2/b2)+(1-as)exp(-d/c)　(3)

　　其中，as(0as1)为快起伏分量在总能量中所占的比例，b、c分别是快、慢起伏分量的去相关距离.这些参数的取值依不同的地物、工作频率和天线极化方式而不同.
　　从时间特性角度考虑，Aq与具有相似分辨单元尺寸的常规脉冲雷达体制下的杂波回波幅度具有相同的时间起伏特性.根据以往的测试研究，在X波段且对于适中的分辨单元尺寸，概率密度分布满足瑞利分布.一般地物的相关函数特性则也是包含了快起伏和慢起伏两种尺度的变化，其归一化时间相关函数为：

R(τ)=atexp(-α2τ2)+(1-at)exp(-βτ)　(4)

其中，at(0at1)为快起伏分量在总能量中所占的比例，α、β分别是快、慢起伏分量的去相关时间.
　　因此，模拟PRC-CW雷达的地杂波回波信号的步骤为：
　　(1)产生一组长度为Q的随机序列［4］，它的概率密度分布满足Weibull分布，而相关性满足式(3)；
　　(2)以上一步产生的Q个数据，作为各子波束回波幅度时间序列的均值mq,从而模拟产生Q组具有式(4)相关特性的相干高斯随机序列，作为各子波束的回波复振幅时间序列；
　　(3)根据式(1)进行迭加，从而得到Vg(t).
　　但是，这样产生的地杂波回波信号尽管考虑到了不同子波束间的空间相关性和同一子波束的时间相关性，但不同子波束间的时间相关性却被认为是互不相关的，这与实际情况有差异，只是时间特性上的一种极端情况.那么，另一种极端情况就是完全相关，而实际情况应介于这两种情况之间.所以，也要考虑完全相关情况下地杂波回波信号，产生步骤是：
　　(1)产生一个子波束的回波复振幅时间序列，它的实部和虚部是相互独立的、但各自满足式(4)相关特性的相干高斯随机序列；
　　(2)在上一步产生的时间序列的基础上，考虑距离衰减，利用式(2)，即可得到Q个子波束的时间序列；
　　(3)根据式(1)进行迭加，从而得到Vg(t).

三、地杂波的时间起伏频谱特性
　　Vg(t)的相关函数为：

RV(τ)=RXX(τ)+RYY(τ)+j［RYX(τ)-RXY(τ)］　(5)

假定Vg(t)可看成是一广义平稳窄带过程，且回波信号的功率谱是一对称谱，则有：RXX(τ)=RYY(τ),RYX(τ)=RXY(τ)=0.所以，RV(τ)=2RXX(τ)，归一化得到相关系数为：rV(τ)=RXX(τ)/RXX(0).对于PRC-CW雷达，发生码元迭加时其相关函数特性，分以下两种情况进行讨论.
　　1.不同波束在时间特性上是相互独立的
　　假定xi、yi、zi、…，(i=0,1,2,…,N-1)分别代表不同波束的回波信号，i代表时间序列中的序号，并且，xi、yi、zi，…，是独立同分布的高斯N(0，σ2)随机变量，有：

E［x2i］=E［y2i］=E［z2i］=…=R(0);
E［xixi+τ］=E［yiyi+τ］=E［zizi+τ］=…=R(τ);
=E［xizi］=E［yizi］=E［xiyi+τ］=E［xizi+τ］
=E［yizi+τ］=…=0

不失一般性，只考虑三个码元迭加后的情况，即：Ai=xi+yi+zi,(i=0,1,…,N-1)，则：

E［A2i］=E［(xi+yi+zi)2］=3R(0);

　　2.不同波束在时间特性上是完全相关的
　　假定xi、yi、zi，…(i=0,1,2,…,N-1)分别代表不同波束的回波信号,i代表时间序列中的序号，并且，xi、yi、zi，…是完全相关的同分布的高斯N(0,σ2)随机变量，有：

E［x2i］=E［y2i］=E［z2i］=…=R(0);
E［xixi+τ］=E［yiyi+τ］=E［zizi+τ］=…=R(τ);
E［xiyi+τ］=E［yizi+τ］=E［xizi+τ］=…=R(τ);

Q个码元迭回后的序列为:
Ai=xi+xi+1+xi+2+…+xi+Q-1,i=0,1,…,N-1
则E[A2i]=QR(0)+2(Q-1)R(1)+2(Q-2)R(2)+…+2R(Q-1)；
E［AiAi+τ］=QR(τ)+(Q-1)R(τ+1)+(Q-2)R(τ+2)
+…+R(τ+Q-1)+(Q-1)R(τ-1)
+(Q-2)R(τ-2)+…+R(τ-Q+1).

仍对相关函数进行归一化，并与没有发生码元迭加时的归一化相关函数相比较：m=E［AiAi+τ］/E［A2i］-R(τ)/R(0).求解此解析式，可得：
　　如果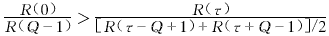成立，则迭加后的相关性将增强，反之，相关性将减弱.分析脉冲雷达的时间相关特性，可知上述不等式都是成立的，所以，在有码元迭加的情况下，如果不同波束间是完全相关时，则时间相关性将增强，且增强的程度取决于上述不等式的差异.
　　因此，对于PRC-CW雷达而言，由于码元和码元之间既不可能完全独立，又不可能完全相关，而是介于其中，所以其时间相关特性也应介于上面两种极端情况之间，也就是说，当码元回波发生迭回时，其时间相关性总是要增强的.
　　通过对相关函数作傅立叶逆变换或利用AR模型，就能得到信号的功率谱密度［5］.

四、地杂波相关特性仿真结果
　　实验中对多种典型地物在PRC-CW雷达下的回波信号进行了计算机模拟，图3～图6分别示出在不同条件下的裸土和油菜的功率谱曲线，它们的空间分布参数及相应的空间相关系数参数、时间相关系数参数列于表1中，采样时间为25微秒.针对不同雷达工作参数得到不同的回波码元迭加次数，进行模拟得到PRC-CW雷达发生码元迭加时的地杂波回波复振幅序列Vg(t)，再分析其频谱特性.

表1　典型地物杂波参数

地物 空间相关参数 时间相关参数 空间分布参数 as b(m) c(m) at α(ms) β(ms) 形参 杂噪比 裸土 0.0 7.89 188.6 0.0 20.0 500.0 3.2 10dB 油菜 0.24 0.30 90.16 0.60 10.0 18.0 2.9 10dB