多相滤波技术在数字相干检波中的应用及FPGA实现

介绍一种利用带通采样定理及多相滤波的方式实现数字相干检波的方法，由于采用数字信号处理的方式获取I、Q基带信号，因此具有镜频抑制能力强、线性动态范围大、系统设备简单、一致性好等优点。文章主要从理论及工程实现两个方面展开论述。

1 基本原理
    设某一数字滤波器的脉冲响应为h(n)，则其Z变换H(z)定义为
  

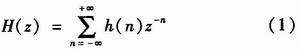
    对式（1）展开变换后，可得
   
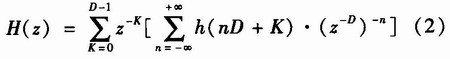
令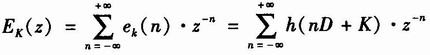则
   
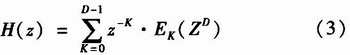
式(2)即为数字滤波器H(z)多相滤波结构，显然H(z)由D个EK(z)，K=0，1，2，…，D-1分支滤波器构成，并且每个滤波器的阶数为H(z)阶数的1／D，这种多相滤波的结构不仅能够提高系统实时处理能力，而且可以降低传统滤波器滤波运算后的累计误差。下面对多相滤波技术在数字相干检波中的应用进行理论分析。
    通常，对于载频为fo的带限(带宽B)中频信号，若以采样率为fs=4fo／(2m+1)，m=O，1，2，…，且fs≥2B对其采样，通过符号修正及多相滤波的方式可准确获得正交的两路基带信号，如图1所示。

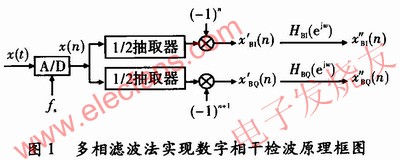
    设信号x(t)=a(t)cos[2πfot+φ(t)]，若以采样率为fs=4fo／(2m+1)，m=0，1，2，…，且fs≥2B对x(t)采样后得到的采样序列为
   
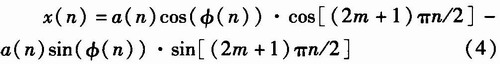
式中，分别为信号的同向分量和正交分量，对x(n)进行奇偶分路和符号变换，可以得到
   
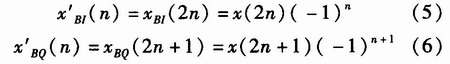
显然，和分别为同向分量和正交分量的2倍抽取序列，容易证明和的数字谱为
   
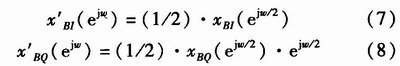
式(7)和式(8)描述了正交解调后同向I及正交Q支路的频谱，但二者的数字谱相差一个延迟因子，这相当于在时域上相差O．5个采样点，需要两个延迟滤波器校正，这两个滤波器需要满足，两路延迟滤波器需要具有相似的幅度或相位特性，保证、支路严格匹配。
    理论分析知，可以采用多相滤波的方式从一原型低通滤波器中取出数字谱相差的两个支路分别对I、Q两路延迟滤波，由于两个滤波器是从同一个原型滤波器中抽取出来的两个分支，因此具有相似的幅度及相位特性。

  设原型滤波器的冲击响应为h(n)，由(1)式知，其多相结构第K条支路的冲击响应为
   
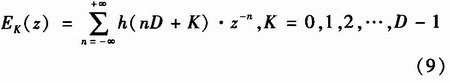
则EK(z)频率响应为
   
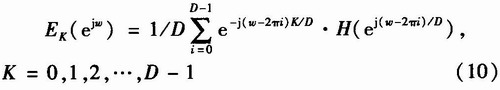
令D=4，则式中除i=0项不为零外，其余均为零，所以求得
   
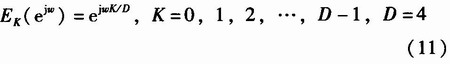
提取K=3及K=1作为式（7）及式（8）I、Q两路延迟滤波，得

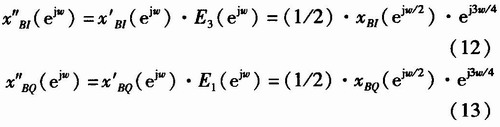
由此可见，经过滤波，两个正交得基带信号在时间上完全对齐，满足数字正交相干检波的要求。

2 仿真分析
    下面采用多相滤波的方法对带宽B=5 MHz，载频fo=60 MHz，信号频率fd的带限信号直接中频采样提取正交的基带分量，采样频率fs=80 MHz，依照多相滤波原理，设计阶数为N，截止频率为B的FIR原型低通滤波器，并从中抽取出数字谱相差两个支路分别对I、Q两路延迟滤波，测试不同频率点的镜频抑制比，仿真测试结果如表1所示。

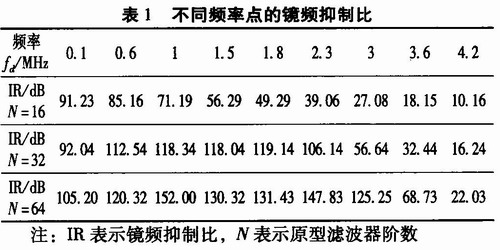
    从数据中可以看出，原型滤波器阶数n越大，镜频抑制比IR越高，fd越大，镜频抑制比IR有下降趋势。图2和图3分别表示N=32，fd=2.3 MHz的及N=64，fd=3 MHz的带限信号相参处理后的功率谱分析。

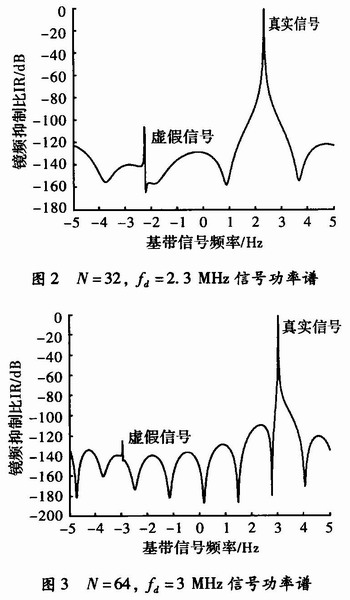
    对于N=32，fd=2．3 MHz的带限信号镜频抑制比IR高达106．14 dB，可见结合带通采样定理及多相滤波方式实现对带限信号直接中频采样获取基带信号能够达到很高的镜频抑制比，这是传统的模拟相干检波难以实现的。
    如上文所述，对宽B=5 MHz，载频fo=60 MHz的线性调频信号直接中频采样，利用多项滤波的方式实现数字下变频仿真输出波形，如图4所示。

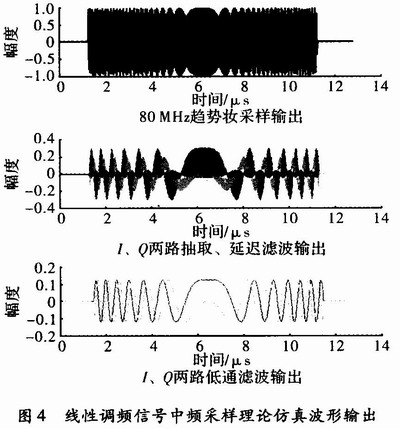
    图4低通滤波输出的是B=5 MHz，时宽T=10μs的基带线性调频信号，从零点的输出看，I、Q两路完全正交。仿真分析表明，利用多项滤波的方式可实现对基带视频信号的提取，完成数字检波的功能。

3 FPGA实现
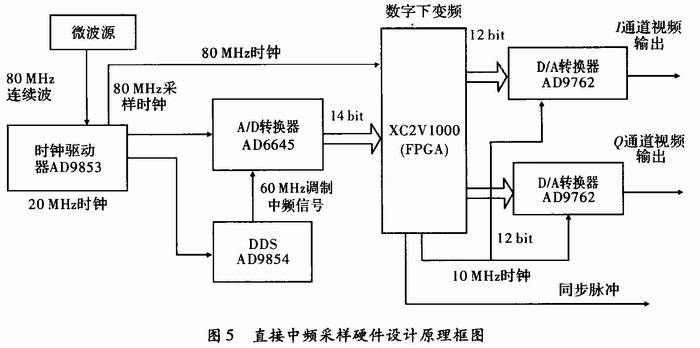
    在一款脉冲压缩体制的雷达中频数字化接收机工程项目中，系统需要实现对带宽B=5 MHz，时宽T=10μs，载频fS=60 MHz的线性调频信号进行直接中频采样，依据带通采样原理，采样频率选为fS=80 MHz。硬件设计原理框，如图5所示。硬件设计中，采用AD9853对微波信号源送的80 MHz的连续波转换为TTL信号的采样时钟及FPGA的工作时钟，同时分频产生20 MHz时钟信号作为DDS芯片AD9854的外部工作时钟，DDS产生60 MHz的脉冲调制的中频信号，A／D转换器采用AD6645，信号和采样时钟同源，具有严格的相位关系，采样后的数字下变频采用Xilinx公司Virtex-Ⅱ系列的XC2V1000来完成，主要包括功能模块为数据的奇偶抽取、符号修正、正交两路延迟滤波，降速抽取、低通滤波以及时序电路设计。

    FPGA设计中，奇偶抽取电路对80 MHz的时钟分频为40 MHz，利用时钟上升及下降沿分别将采样后的I(0)、Q(1)、I(2)、Q(3)……的序列进行奇偶抽取，对抽取的正交两路数据分别进行符号修正，修正的目的主要是解决采样时符号反向的问题，符号修正电路实现可通过对采样时钟4分频，高电平时I、Q两路数据分别保持不变，低电平时，I、Q两路数据求其每一位逻辑反后加1，功能上相当于乘以-1，修正后的两路输出序列分别为I(0)、I(2)、I(4)、Q(6)……及Q(1)、Q(3)、Q(5)、Q(7)……，由上述理论分析知，两路数据在时间上相差一个采样点，对于数字频率相差个相位，需要通过延迟滤波器来实现时间上对齐，延迟滤波器采用多项滤波的方式实现，即I、Q两路的滤波器的系数由同一个原型滤波器设计而成，FPGA中滤波器设计采用Xilinx的IP核中的FIR模块，延迟滤波后的数据经4倍降速抽取，并通过低通滤波器滤除高阶分量后送外部D／A变换器，低通滤波器采用32阶的FIR数字滤波器，滤波器设计同样采用IP核实现，FPGA设计原理框，如图6所示。

4 结束语
    文中讨论了直接中频采样下，利用多相滤波的方法实现数字检波的基本原理及实现方法，并给出FPGA实现的工程样例。计算机仿真表明，利用带通采样定理及多相滤波方式对带限信号直接中频采样能够准确可靠地将一定带宽范围内的基带信息提取出来，而且相对传统的模拟相干检波能够获得较高的镜频抑制比，利用FPGA单片资源便可实现单通道甚至多通道的数字相干检波的功能，简化了系统设计，而且在技术指标上又可有效地克服正交通道不一致的问题，具有较高的工程应用价值。欲了解更多信息请登录电子发烧友网(http://www.elecfans.com)