
各队解决方案综述
文献[1]提出的方法是:可以通过对于每行提取的道路位置通过一个线性修正来消除梯形失真,可通过实验的方式确定线性补偿的系数。但是该实验方法比较繁杂,并且不能消除桶形失真。
文献[2]制作了一个图像标定板,如图1所示。

其原理是:图1(a)中阴影部分是车体放置的位置。在标定板上等间距地贴了许多黑线,给标定板拍照后,就可以知道实际中的位置与图像中的位置的相互关系。这个方法由于黑线有一定宽度,所以会存在较大误差。
文献[3]采用非均行采集的方案。所谓非均行采集是与均行采集对应的。在均行采集中,AD模块所采集的行均匀分布于摄像头输出的图像中。而非均行采集则是指,AD模块所采集的行按某种规则非均匀地分布在原始图像中,而这种规则是保证采集得到的图像在纵向上(小车中轴方向)与现实景物不畸变。然后再确定每一行的横向畸变系数。

如图2所示,非均行采集时,远处采得密,近处采得稀。由于摄像头安装方式在实验时会经常变动,以确定最佳俯角和最佳高度,每当变动就需要重新标定。这个方案就不大方便了。文献[4]建立了一个光路几何模型图,如图3所示。

实验方案:量取摄像头架固定螺钉的高度H与摄像头中心相对于竖直杆的偏转角度(俯角)θ。由于光学中心的计算完全由这两个数据及近端距固定杆的距离S(即测量保险杠距固定杆的距离S0和近端距保险杠距离S'相加得到,也可直接在实验板上测量由近端黑线到摄像头固定杆的距离S)确定,因此要做到越精确越好。由O点做垂线长度为H至点A,做水平线AB,截取AD长为S,DB过O点做与垂直线成θ的射线交AB于C,过D做DE垂直于OC,并使OC为DE的垂直平分线,连接BE并延长,交OC与O’,则O’为光学中心。从图上能算得O’距底边距离为H’,俯角不变。将实验板垂直放置,做出边长为A1的正方形标定区域,即图3中的DE平面,将摄像头水平对向实验板中心C,摄像头架固定螺钉距实验板距离为H1。读出标定实验板上特征点的相应像素点。可以得到图4中(X,Y)与像素点(U,V)的关系(U为行数,V为列数)。
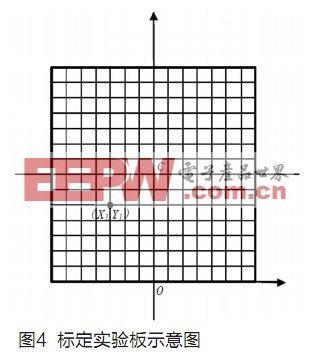
由于实验平面与真实视野平面之间是纯几何关系,因此这部分转换函数关系可以用几何推导。 其公式较复杂,在这里不一一列出。
其公式最大的弊端在于有很多sin()、cos()等三角函数运算,但单片机做这种运算会花费大量时间,所以本应尽量避免出现三角函数、开方等运算。而且,若采用广角镜头或摄像头架得较低时,B点将会距A点很远而找不到B点。所以该方法也不具通用性。实验本身也比较复杂。
文献[5]采用的实验方法是:事先在一块白板上画一系列小的正方格,正方格越小,精度越高。然后标定中心黑粗线,用来确定赛车的摆放位置和图像的中心。如图5所示。之后可以直接读出各特征点相应的像素坐标,建立对应关系。

该实验方案很直观,但其 *** 作未必简便。因为摄像头视野较广,所需矫正网络也较大,在其上画方格线很难保证绝对水平或垂直。
文献[6]根据几何数学建模,得出摄像头获取图像的成像坐标与景物实际的世界坐标的关系。坐标变换关系如下:

在摄像头安装固定后,c/tanθ、a、b、c、h 和h/cosθ 均为常量。这个方法还是比较好的,但是需要知道f、L、H,这三个参数厂家会提供,但不一定准确,θ也较难准确测量,且不能解决桶形失真的问题
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)