存储深度对FFT结果的影响

存储深度对FFT结果的影响

    在DSO中，通过快速傅立叶变换（FFT）可以得到信号的频谱，进而在频域对一个信号进行分析。如电源谐波的测量需要用FFT来观察频谱，在高速串行数据的测量中也经常用FFT来分析导致系统失效的噪声和干扰。对于FFT运算来说，示波器可用的采集内存的总量将决定可以观察信号成分的最大范围（奈奎斯特频率），同时存储深度也决定了频率分辨率△f。如果奈奎斯特频率为500 MHz，分辨率为10 kHz，考虑一下确定观察窗的长度和采集缓冲区的大小。若要获得10kHz 的分辨率，则采集时间至少为： T = 1/△f = 1/10 kHz = 100 ms，对于具有100 kB 存储器的数字示波器，可以分析的最高频率为：

△f × N/2 = 10 kHz × 100 kB/2 = 500 MHz

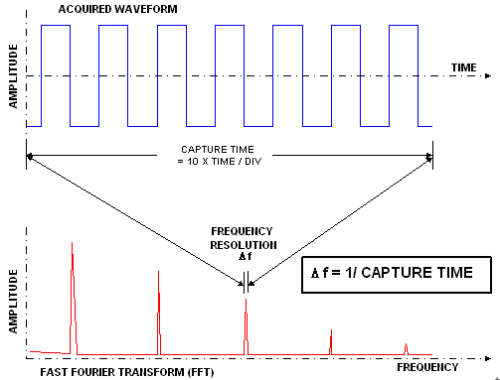
图11 示波器的FFT运算

在图12所示的例子中，266 MHz信号受到来自30 kHz噪声源的捡拾噪声的影响。FFT (下方的轨迹)显示了以266 MHz为中间、相距30 kHz的一系列峰值。这种失真十分常见，可能是由于开关式电源、DC-DC转换器或其它来源的串扰导致的。它也可能是由故意使用扩频时钟导致的。

图12 力科示波器的FFT分析

对于DSO来说，长存储能产生更好的FFT结果，既增加了频率分辨率又提高了信号对噪声的比率。另外，针对某些应用，一些非常细节的信息需要在20Mpts的存储深度下才能分析出来，如图13、14所示。

图13 1M点的FFT结果无法了解有关调制的信息

图14 20M点的FFT清晰的确认了时钟的双峰分布及相关调制规律

    需要指出的是，对于长波形的FFT分析需要示波器超强的数据处理能力，这往往超出了某些示波器的运算极限。力科示波器最大可以做25M点的FFT，业内T公司的示波器最大则只能做3.125M点的FFT分析。