
回到仪表放大器的简化模型(如图 1 所示)中,我们可以再次回想起 PSRR 与 CMRR 都是输入参考参数。
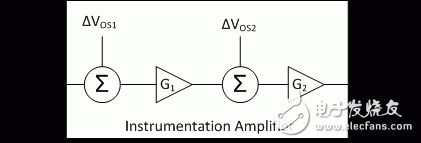
图 1:仪表放大器的概念模型
在更高的增益下,当需要计算输入时,可用输入级增益除以第二级失调的变化:
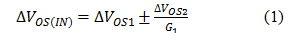
这里就是二级放大器概念模型不完备的地方。例如:如果两个二级放大器的失调变化相同,而且极性也相同时会怎样呢?也就是说:
对比增益为 1000 及增益为 1 的放大器在 PSRR 方面的改善情况:
如果输入参考失调变化减少一半,PSRR 就可提高 6dB。但是在将增益从 1 提升至 1000 时,典型仪表放大器的 PSRR 可能会提高达 30dB。显然,ΔVOS1 必须远远小于 ΔVOS2 才能实现这种水平的改善。
我们通过仔细观察图 2 中三运算放大器仪表放大器的内部结构便可明白如何实现这种可能性。由放大器 A3 和电阻器 R3、R4、R5 以及 R6 组成的输出级可作为差分放大器配置。如果电阻器 R3、R4、R5 和 R6 符合以下比例:
那么输出级就将只放大输入级的差分电压,抑制两个输入端的共模。

图 2:三运算放大器仪表放大器的标准拓扑
放大器的输入级包含两个放大器:A1 和 A2。电源电压或共模电压的变化会带来这两个放大器输入失调的相应变化,在图 3 中分别使用 ΔVOS1A 和 ΔVOS1B 表示。
图 3:仪表放大器的输入级放大器及其各自的失调情况
让我们来看看这种情况,A1 和 A2 的非反相输入接地,并将输入级增益配置为 1。现在,假设电源电压的变化会导致 A1 和 A2 的输入失调电压发生变化。那么,接地的每个放大器输出都将在失调电压中反映出这种变化。输入级的输出共模电压将为:
而输出差分电压则将为:
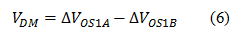
前面已提到过输出级差分放大器抑制共模电压,只有差分电压可传输至输出端。因此,输入级的输入参考失调变化 (ΔVOS1) 实际上由 ΔVOS1A 与 ΔVOS1B 之差决定,而非其绝对量级!
通过对 IC 进行精心设计与布局,这两种失调就可获得良好的匹配,从而可将输入级失调变化平均降至输出级的大约十分之一。
仪表放大器的 CMRR 与 PSRR 参数不会如魔法般地随增益提高而改善,事实上它是多级拓扑与差分放大器输出级的结果。
输入放大器的精确匹配与输出级电阻器的正确布局有助于现代 IC 仪表放大器为电子工程师提供我们已习以为常的巨大抑制功能。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)