卡尔曼滤波器及多传感状态融合估计算法

      采用CarlsON 最优数据融合准则， 将基于Kalman 滤波的多传感器状态融合估计方法应用到雷达跟踪系统。仿真实验表明，多传感器Kalman 滤波状态融合估计误差小于单传感器Kalman 滤波得出的状态估计误差，验证了方法对雷达跟踪的有效性。

　　随着科学技术的发展， 特别是微电子技术、集成电路技术、计算机技术、信号处理技术及传感器技术的发展， 多传感器信息融合已经发展成为一个新的研究领域， 并在军用领域和民用领域均得到了广泛应用。

　　多传感器信息融合的基本原理如同人脑综合处理信息的过程， 即充分利用多个传感器资源， 通过对各种传感器及其观测信息的合理支配与使用， 将各种传感器在空间和时间上的互补与冗余信息依据某种优化准则组合起来， 从而得出更为准确、可靠的结论。

　　现代战争的多样性和复杂性提出了对信息处理更高的要求， 信息融合可对多传感器提供的多种观测信息进行优化综合处理， 从而获取目标状态、识别目标属性、分析目标意图与行为， 为电子对抗、精确制导等提供作战信息。本文将基于Kalman 滤波的多传感器状态融合估计方法应用到雷达跟踪系统。仿真实验表明， 三个传感器融合所获得的估计值都更加贴近于目标信号， 因而提高了对雷达系统的跟踪精度。

　　1 卡尔曼滤波器

　　多传感信息融合的主要任务之一就是利用多传感器信息进行目标的状态估计。目前， 进行状态估计的方法很多，Kalman 滤波器是一种常用方法。Kalman 滤波器在机动目标跟踪中具有良好的性能， 它是最佳估计并能够进行递推计算， 即它只需要当前的一个测量值和前一个采样周期的预测值就能进行状态估计。

　　考虑一个离散时间的动态系统， 它有如下形式：

　　针对动态系统(1) 和(2) ，Kalman 递推滤波算法如下：

 

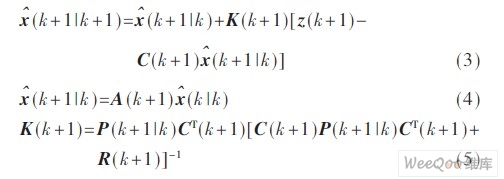
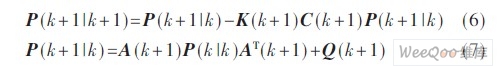
　　2 多传感状态融合估计算法

　　单采样率多传感器状态融合估计的研究方法主要有基于概率论的方法、基于Kalman 滤波的方法、基于推理网络的方法、基于模糊理论的方法、基于神经网络的方法， 以及基于小波、熵、类论、随机集、生物学灵感、Choquet 积分的方法等等。基于Kalman 滤波的方法由于具有 *** 作简单、计算量小、实时性强等优点， 得到最为广泛的研究。

　　下面重点介绍基于Kalman 滤波的分布式数据融合状态估计算法。设多传感器系统有如下形式：

　　状态向量初始值x(0)为一随机向量， 并且有：

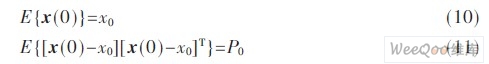
　　假设x (0)、w (k) 和v (i，k) 之间是统计独立的，i =1，2，…，N 表示传感器。数据融合的目的是通过合理利用这些传感器的观测信息， 获得状态的最优估计值。

　　Carlson 在1990 年提出了一种最优数据融合准则。

　　设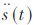分别表示状态基于传感器i 观测信息的Kalman 滤波估计值和相应的估计误差协方差阵， 对于i=1 ，2，…，N， 假设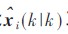不相关， 则最优联邦滤波器最优数据融合准则由下式给出：

　　其中：

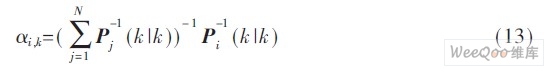
　　相应的估计误差协方差矩阵为：

　　可以证明：

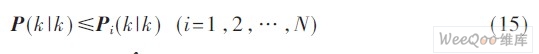
　　其中P(k|k)表示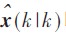的估计误差协方差。

　　基于第i 个传感器信息的Kalman 滤波估计器如图1 所示。Carlson 联邦融合估计算法流程图如图2 所示。

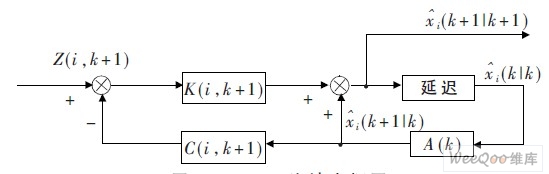
图1 Kalman 滤波方框图

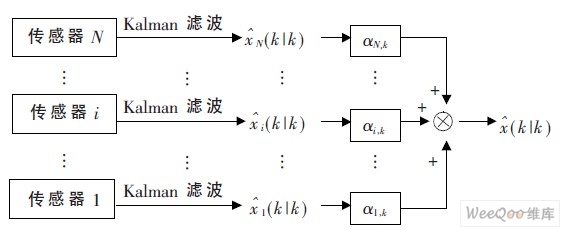
图2 联邦融合估计算法流程图

　　3 雷达跟踪系统仿真

　　考虑具有3 个传感器的雷达跟踪常加速度模型，其离散状态方程为：

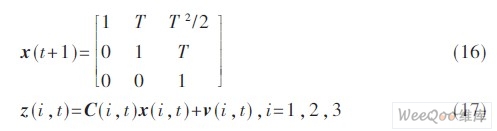
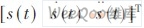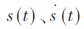　　式中T 表示采样间隔。状态向量x(t)=，其中和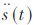分别表示目标在tT 时刻的位移、速度和加速度。z(i，t)(i=1 ，2，3) 表示3 个传感器的观测，它们分别观测位移、速度和加速率。即：C(1)=[1 0 0] ，C(2)=[0 1 0] ，C(3)=[0 0 1] 。v(i，t) 和w(t) 分别是观测误差和系统误差， 都假设为零均值的高斯白噪声， 方差分别为R(i)和Q。本节的目的是融合3 个传感器的观测信息， 以获得对目标x(t)的最佳估计。这里T=0.01 s ，Q=0.1 ，R(3)=20 ，R(2)=15 ，R(1) =8 。初始值为x (0) =[0 1510] 和P0=0.1·I3。

　　设传感器的采样点数为600 ， 则10 次Monte Carlo仿真的统计结果如表1 所示。表1 给出了估计误差绝对值均值比较，3 个传感器融合的综合估计误差是最小的。

表1 估计误差绝对值均值比较。

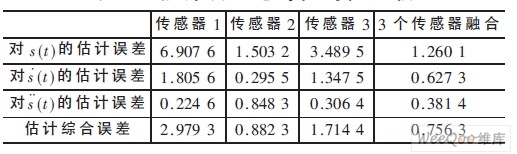
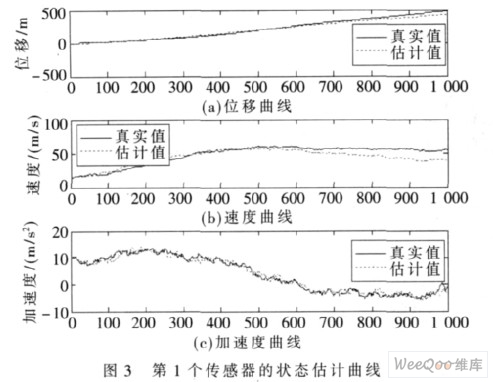
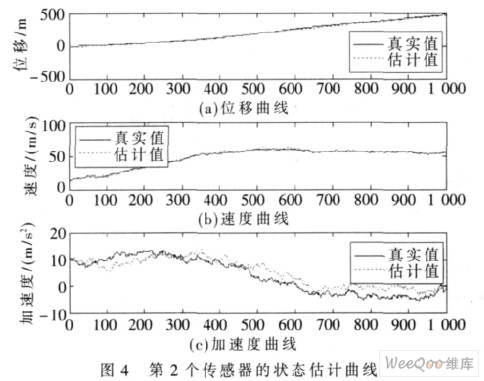
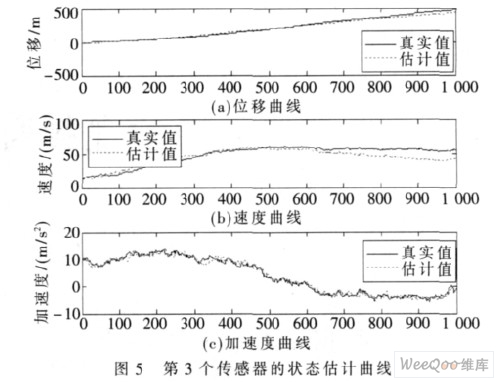
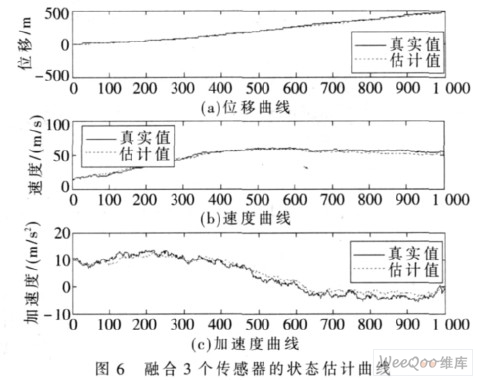
　　第1 个传感器、第2 个传感器、第3 个传感器及3个传感器融合的状态估计曲线分别如图3、图4、图5、图6 所示。图中横轴为仿真步数， 每步时间为0.01 s 。若仔细观察这些状态估计曲线，则单传感器状态估计曲线均有不足， 如图3 对速度跟踪不是很好， 图4 对加速度跟踪不是很好， 图5 对速度跟踪也不是很好， 只有图6对位移、速度及加速度跟踪均较好。由此可见， 与单传感器Kalman 滤波的结果相比，3 个传感器融合所获得的估计值都更加贴近于目标信号，从而证明了本文算法的有效性。

　　信息融合技术具有提高系统的可靠性和稳定性等优点， 状态融合估计是其中研究热点之一。本文将基于Kalman 滤波的多传感器状态融合估计方法应用到雷达跟踪系统， 仿真实验表明， 融合3 个传感器的信息所获得的状态估计误差小于利用任何单传感器进行Kalman滤波得出的状态估计误差， 因而本方法对雷达系统的跟踪是很有效的。本方法可推广用于组合导航、信号处理、图像处理、故障检测与容错等应用领域。