
O 引 言
模拟滤波器的设计一般包括两个方面:根据技术指标即滤波器的幅频特性确定滤波器的传递函数H(s);设计实际网络实现这一传递函数。设计滤波器H(s)的关键是找到逼近函数,目前已有多种逼近函数。然而,不论哪种逼近函数都需要进行非常繁琐的计算,还要根据计算结果进行查表。
Matlab语言是一种简单、高效的高级语言,是一种内容丰富、功能强大的分析工具,其应用范围几乎覆盖了所有的科学和工程计算领域。Matlab中提供了丰富的用于模拟滤波器设计的函数,通过编程可以很容易实现低通、高通、带通、带阻滤波器,并能画出滤波器的幅频、相频特性曲线,大大简化了模拟滤波器的设计。在此介绍了用Matlab设计实现一个无失真模拟滤波器,并给出了幅频、相频特性的仿真结果和信号通过无失真滤波器后的眼图。
1 基于Matlab的无失真滤波器设计
设计要求:一个频率为8 kHz数字基带信号经过数/模(D/A)转换后得到一个模拟信号,将该模拟信号输入无失真滤波器,要求在8 kHz频率处衰减为~6 dB;在16 kHz频率(截止频率)之后衰减达到一60 dB以上。这样做的目的是使该模拟信号经过无失真滤波器后,抑制谐波干扰,减小截止频率后波形的起伏。
无失真滤波器由三部分组成,依次为低通滤波器、带阻滤波器、相移电路。其中低通滤波器的作用是通过8 kHz以内的低频信号;带阻滤波器的作用是抑制16 kHz信号,它与前面低通滤波器级联后能使16 kHz之后信号的衰减达到一60 dB以上,有效地抑制各次谐波干扰,并减小16 kHz之后波形的起伏;相移电路的作用是补偿前面两级电路的相位偏移,使得整个无失真滤波器的相位特性成为一条直线。
1.1 低通滤波器设计
低通滤波器采用巴特沃斯型滤波器,因为它具有较平坦的幅频特性,相频特性线性较好,常作为滤波器的初级。在Matlab中,用[b,a]=butter(n,wn,‘s’)语句来实现巴特沃斯滤波器的设计。其中,[6,a]是滤波器传递函数多项式的系数;n为滤波器的阶数;wn为3 dB处的角频率;‘s’表示模拟滤波器的。
在该设计中,采用8阶巴特沃斯滤波器,一3 dB处的频率为8 kHz。主要程序如下:

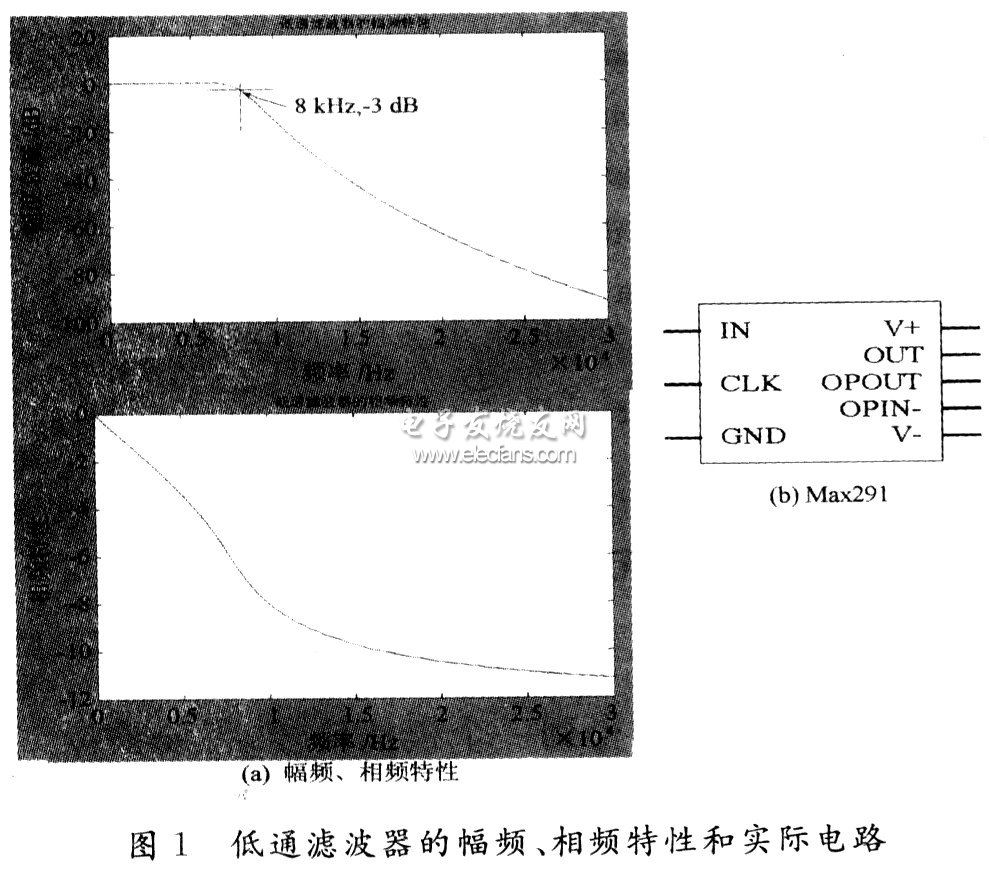
最终画出低通滤波器的幅频、相频特性如图1(a)所示。实际电路采用由Max291芯片来实现巴特沃斯滤波器,它相当于8阶巴特沃斯滤波器,如图1(b)所示。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)