
什么是决策树
决策树是预测模型。先举一个简单的决策树的例子。
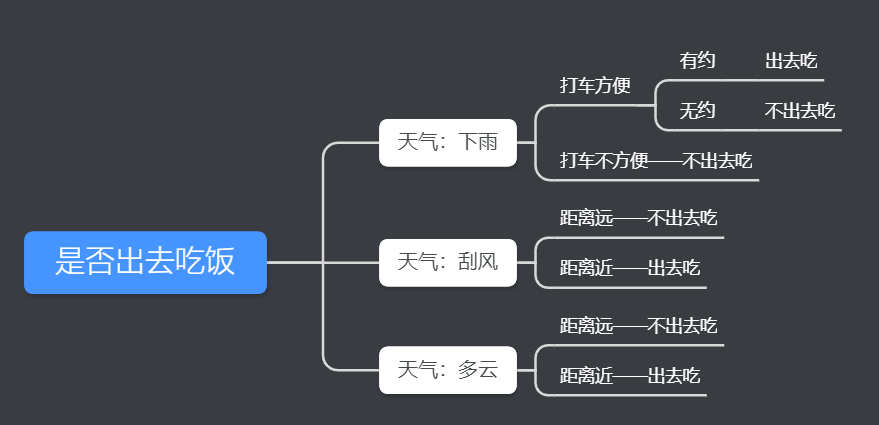
在这个例子中,我们考虑是否出去吃饭,需要经过以下考虑。
如果天气下雨,就考虑打车是否方便。如果打车方便,就要看是否和别人有约。如果有约,就出去吃,如果无约,就不出去吃。
如果天气刮风,就看目的地远近。如果距离远,就不出去吃。如果距离近,就出去吃。
如果天气多云,就看目的地远近。如果距离远,就不出去吃。如果距离近,就出去吃。
这个过程就是决策树。
天气、打车是否方便、距离远近、是否有约等要素称为特征(features)。
出去吃和不出去吃,就是特质值下的分类(target)。
决策树的判断标准
在决策树中,可能有多个特征,但是一些特征是无关重要的,一些则是对分类(target)起到决定作用的。
比如,在上例中,下雨、刮风和多云影响我们是否出去吃饭,但还有其他不影响我们是否出去吃的因素。
那我们选择哪个因素作为分类标准呢?我们有两种方法,一种叫做信息熵(音同“商”),一种叫做基尼不纯度。
信息熵模型
信息熵(entropy)是指信息包括的信息量,也就是信息量的大小。
信息量和什么相关呢?分别是该信息对别人有没有用,和信息表达的事情会不会发生。
试想,如果我们和别人说了一件根本不会发生的事,那是不是一句废话,也就是说,信息量为0。
比如,我们告诉别人,你老板年终奖会给你发100万,这件事虽然是听者关心的,但是如果不会发生,那信息量也为0。
但如果我们和别人说了一件未来一定会发生的事情,那如果这件事对别人来说一点用也没有,信息量也为0。
比如,我们告诉别人,你明年一定会长一岁。这件事虽然一定会发生,但是对听者没有意义,因此信息量为0。
因此,我们定义信息熵,用h(x)——信息有没有用和p(x)——信息可能发生的概率表示。
信息熵
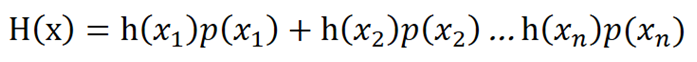
我们再来看h(x)和p(x)有什么关系。也就是一件事的信息量和发生概率的关系。
通常来说,一件事情发生概率越低,那么信息量越大。
比如,如果有人告诉你明天彩票的中奖号码,那这件事十分重要,但发生的概率也非常低。
如果一件事是必然发生的,那这件事的信息量也十分有限。比如有人告诉你第二天太阳会升起,这件事其实没什么用。
因此,我们可以得到以下结论:
1.h(x)和p(x)是负相关的;
2.p(x)=1,h(x)=0;
3.p(x)=0, h(x)是无限大的。
此外,
如果一件事x1发生的概率是p(x1),第二件事x2发生概率是p(x2)……第n件事xn发生概率事p(xn),
那么x1,x2……xn共同发生的概率是p(x1)p(x2)……P(xn)
如果一件事x1的重要性是h(x1),第二件事x2的重要性是h(x2)……第n件事xn的重要性是h(xn),
那么x1,x2……xn的重要性是h(x1)+h(x2)……h(xn)
综上所述,h(x)和p(x)满足log(x)的函数形式,考虑到p(x)=0时,h(x)无限大,因此还需要加一个负号。因此我们设定h(X)=-log(p(x))
一般情况下,我们假定log的底数为2。就有
h(x)=-log2(p(x))
为什么要选择以2为底呢?
假设一个事件的信息量是n个相互独立随机变量发生的结果,其中每一个选择都在“是”或“否“之间做出,则所有可能结果数为N=2^n,n= log2(N)
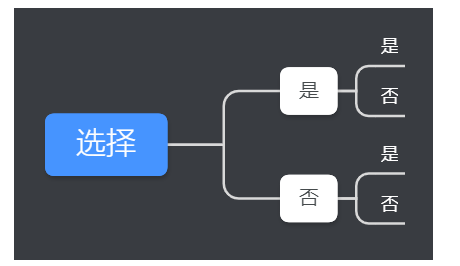
返回最开始的信息熵。
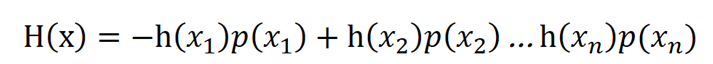
将h(x)和p(x)的关系代入,我们就有:
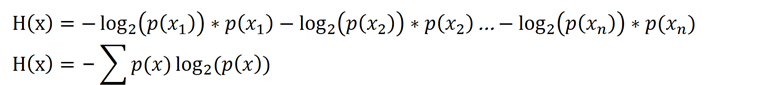
决策树的算法
有了上面信息熵,我们就能根据信息熵选择特征,也就是选择哪些因素作为决策树的分类的判断标准。
选择方法有两种,一种是根据信息增益,一种是根据信息增益率。
ID3算法
信息增益的概念很简单,整体的信息熵减掉以按某一特征分裂后的条件熵。
也就是说,我们按照某一个特征进行分类,来观察信息熵的变化。若信息熵的变化足够大,那这个特征就会被选中。信息熵的变化称为信息增益。
信息增益
这种根据信息增益选定特征的算法叫做ID3。
ID4.5算法
但是根据信息增益来判断特征会有一个缺点。信息增益会受到特征数量的影响。特征数量越多,信息熵越大,那剔除某些特征后的信息增益越大。当特征的取值较多时,根据此特征划分之后的熵更低,由于划分前的熵是一定的,因此信息增益更大,因此信息增益比较 偏向取值较多的特征。极端一点,有多少个样本,这个特征就有多少个类别,那么就会导致决策树非常浅。
那如何处理这个问题呢?我们选择增加一个惩罚项。
这个惩罚项就是H(D)。
信息增益率:
GainraTIo(D,A) = Gain(D,A)/H(D)
这种根据信息增益率选定特征的算法叫做ID4.5。
CART算法
不管是ID3还是ID4.5,他们都有一个问题,就是不能处理回归问题。
因此,产生了新的算法,CART算法。
CART是采用基尼系数(基尼不纯度),选取最优划分特征。
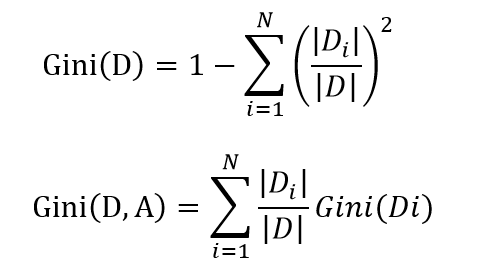
责任编辑人:CC
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)