什么是格雷码

 

　　格雷码(Gray code),又叫循环二进制码或反射二进制码 在数字系统中只能识别0和1，各种数据要转换为二进制代码才能进行处理，格雷码是一种无权码，采用绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便。格雷码属于可靠性编码，是一种错误最小化的编码方式

　　简介

　　因为，自然二进制码可以直接由数/模转换器转换成模拟信号，但某些情况，例如从十进制的3转换成4时二进制码的每一位都要变，使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它是一种数字排序系统，其中的所有相邻整数在它们的数字表示中只有一个数字不同。它在任意两个相邻的数之间转换时，只有一个数位发生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。另外由于最大数与最小数之间也仅一个数不同，故通常又叫格雷反射码或循环码。

　　二、格雷码对照表

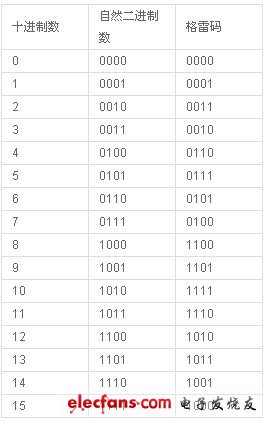
　　下表为几种自然二进制码与格雷码的对照表：

　　一般的,普通二进制码与格雷码可以按以下方法互相转换:

　　二进制码->格雷码(编码)：从最右边一位起，依次将每一位与左边一位异或(XOR)，作为对应格雷码该位的值，最左边一位不变(相当于左边是0);

　　格雷码-〉二进制码(解码)：从左边第二位起，将每位与左边一位解码后的值异或，作为该位解码后的值(最左边一位依然不变).

　　数学(计算机)描述：

　　原码：p[n:0];格雷码：c[n:0](n∈N);编码：c=G(p);解码：p=F(c);

　　书写时按从左向右标号依次减小,即MSB->LSB，编解码也按此顺序进行

　　编码：

　　...................c[n]=p[n]，

　　...................c[i]=p[i] XOR p[i+1] (i∈N,n-1≥i≥0);

　　解码：

　　...................p[n]=c[n]，

　　...................P[i]=c[i] XOR p[i+1] (i∈N, n-1≥i≥0)。

　　Gray Code是由贝尔实验室的Frank Gray在20世纪40年代提出的(是1880年由法国工程师Jean-Maurice-Emlle

　　Baudot发明的)，用来在使用PCM(Pusle Code ModulaTIon)方法传送讯号时避免出错，并于1953年3月17日取得美国专利。由定义可知，Gray Code的编码方式不是唯一的，这里讨论的是最常用的一种。

　　用异或乘除法实现二进制码与格雷码互相转换

　　如果在二进制运算中忽略进位、退位，那么加减运算都变成了异或(XOR)。

　　用异或代替加减进行二进制竖式乘除，称为异或乘除，它的特点是无进退位。

　　由于没有退位，异或除法将变得更像多项式除法。

　　如：10101除以11将变成1100余1，而不是111。

　　二进制转格雷码：

　　只要异或乘以二分之三，即二进制的1.1，然后忽略小数部分;也可以理解成异或乘以三(即11)，再右移一位。

　　格雷码转二进制：

　　异或乘以三分之二，即除以1.1，忽略余数;或者左移一位，再异或除以三，忽略余数。