格雷码辨析

　  格雷码( Gray Code,GreyCode,又称作葛莱码，二进制循环码) 是1880 年由法国工程师Jean - Maurice - Emlle Baudot 发明的一种编码，因Frank Gray 于1953 年申请专利"Pulse CodeCommunicaTION"而得名。当初是为了机械应用，后来在电报上取得了巨大发展，现在则常用于模拟- 数字转换和转角- 数字转换中。

　　1 格雷码( Gray Code) 的由来

　　无容置疑，迄今为止对典型格雷码( Primary GrayCode) 的权威描述是Frank Gray的美国专利"PULSECode CommunicaTIon[8]".该专利申请于1947 年11 月13 日，申请号为785697; 1953 年3 月17 日获得批准，专利号为2632058,专利权归贝尔电话实验室所有。

　　根据所用编码的镜像反射特性，专利将其称之为反射二进制码( Reflected Binary Code) .专利还介绍了几种变形格雷码( Gray Code Variants)。

　　笔者所见最早使用术语"Gray Code"的文献是Earl Albert Ragland 等人在1953 年10 月16 日申请、1958 年2 月11 日获得批准的2823345 # 美国专利"DirecTIon - SensiTIve Binary Code Position Control System[9]".据此，Gray code 出现在1953 年10 月16 日之前在逻辑上是可能的。另一篇使用Gray Code 的文献是Jack Breckman 在1953 年10 月31 日申请、1956 年1 月31 日获得批准的2733432 # 美国专利"EncodingCircuit".考虑到专利公开时的修订问题，GrayCode 的出现应不晚于1956 年1 月。

　　2 格雷码的特点和应用

　　典型的二进制格雷码( Binary Gray Code) 和部分其他数码如表1 所示。

　　表1 典型二进制格雷码和其他部分数码

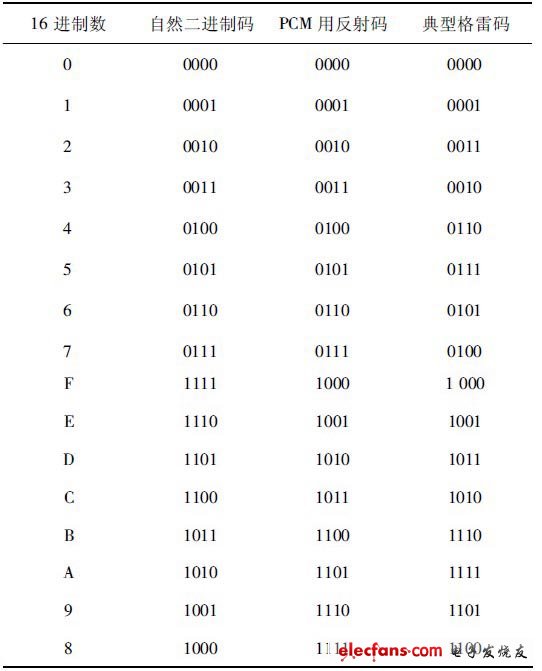
　　典型格雷码是具有反射特性和循环特性的单步二进制自补码( Reflected Cyclic Binary Unit - diSTanceSelf - complementing Code) .与自然二进制码( NaturalBinary Code) 相比，它的误码率较低，是一种错误最小化的可靠性编码，又称为最小差错〔二进制〕码( Minimum Error [binary]Code) ,经常用在数字通信和自动化测控系统中，使用在格雷码计数器中还可以大大降低计数器的动态功耗。格雷码还与PDC( Position - to - Digital Converter) 、TDC、ADC、DAC、真值表、卡诺图、哈密顿图、九连环、汉诺塔、十六进制难题( Hexadecimal Puzzle) 、回形滑行难题或疯像跳舞( Spinout Puzzle or Crazy Elephant Dance) 等数字测控、数理逻辑和人工智能问题有着密切关系。利用格雷码的奇偶性和± 1 规律等数学性质，可以方便地设计出可级联、可预置、可逆计数的三可格雷码计数器，也方便了九连环的套解和汉诺塔的搬移。

　　3 几个错误说法

　　尽管有很多专家学者对格雷码的研究和发展做出了巨大贡献，但难免也会出现一些不太准确的说法。

　　现归纳如下：

　　( 1) 将Gray Code 说成无权码。

　　在Gray 的专利中可知其权的绝对值为2n - 1,其符号按照1 出现的次序从高到低正负交替。可能是因为无数学推导，且在专利中有3 处误写为2n - 1 而不符合实际情况( 在Robert L. Carbrey于1948 年2 月10 日申请、1951 年1 月16 日获得批准的2538615#专利中写法都是正确的) ,致使很多数字电子技术和计算机技术的文献认为格雷码是无权码，仅互动百科称其为准权码,汪蔚霄给出了与Gray 类似的权值，J. F. A. Thompson 认为可以从格雷码直接转换成十进制数[22].

　　( 2) 将Gray code 写成Grey Code或Gray Code.

　　美语gray 等同于英语grey 是"灰色"的意思，且Gray 和Grey 的人名音译均为格雷，因而造成错用。但Gray Code 因Frank Gray 命名，绝不能写成Grey Code;可写为Gray code,但不能写成gray code.