
由于高等数学底子太差的原因,机器学习无法深入学习下去,只能做一个简单的尝试者,甚至连调优也未必能算的上,不过这样也好,可以把重心放到对业务的理解上,以及业务和模型的选择上。
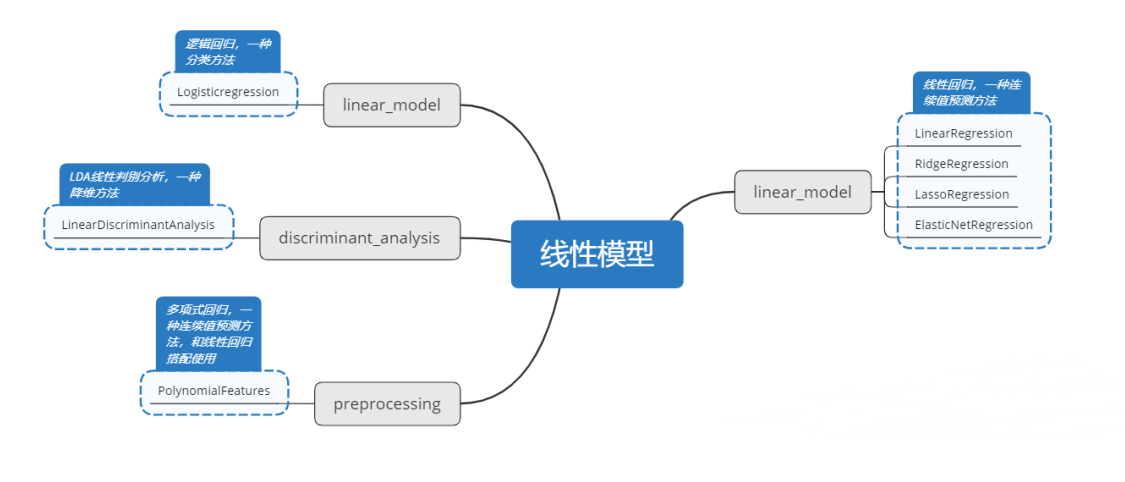
线性模型包括了传统的线性回归、岭回归、Lasso回归,主要用于连续值的预测;逻辑回归虽然也是回归,但却是一种分类方法;LDA线性判别分析,则是一种降维方法;多项式回归,是使用线性模型训练数据的非线性函数。
总的来说,尝试着回顾一下,也挺有意思的。
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model,discriminant_analysis,model_selecTIon,preprocessing
from sklearn.pipeline import make_pipeline,Pipeline
def load_data():
diabetes=datasets.load_diabetes()
# datasets.load_diabetes()定义
# C:\Python\Python37\Lib\site-packages\sklearn\datasets\_base.py
# return Bunch(data=data, target=target, DESCR=fdescr,
# feature_names=['age', 'sex', 'bmi', 'bp',
# 's1', 's2', 's3', 's4', 's5', 's6'],
# data_filename=data_filename,
# target_filename=target_filename)
# print(diabetes)
# 得到一个字典
# print(diabetes.keys())
#dict_keys(['data', 'target', 'DESCR', 'feature_names', 'data_filename', 'target_filename'])
# print(diabetes['data'].shape)
# (442, 10)
# print(diabetes['target'])
# print(diabetes['target'].shape)
# (442, )
# print(diabetes['feature_names'])
# ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
# print(diabetes['data_filename'])
# C:\Python\Python37\lib\site-packages\sklearn\datasets\data\diabetes_data.csv.gz
# 压缩包中有个X.csv文件,数据格式如下
# 3.81E-02 5.07E-02 6.17E-02 2.19E-02 -4.42E-02 -3.48E-02 -4.34E-02 -2.59E-03 1.99E-02 -1.76E-02
# -1.88E-03 -4.46E-02 -5.15E-02 -2.63E-02 -8.45E-03 -1.92E-02 7.44E-02 -3.95E-02 -6.83E-02 -9.22E-02
# 8.53E-02 5.07E-02 4.45E-02 -5.67E-03 -4.56E-02 -3.42E-02 -3.24E-02 -2.59E-03 2.86E-03 -2.59E-02
# print(diabetes['target_filename'])
# C:\Python\Python37\lib\site-packages\sklearn\datasets\data\diabetes_target.csv.gz
# 压缩包中有个y.csv文件,数据格式如下
# 1.51E+02
# 7.50E+01
# 1.41E+02
return model_selecTIon.train_test_split(diabetes.data,diabetes.target,
test_size=0.25,random_state=)
# 线性回归
def test_LinearRegression(*data):
X_train, X_test, y_train, y_test = data
# 线性回归模型-最小二乘法线性回归:
# sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False,copy_X=True, n_jobs=1)
# 主要参数说明:
# fit_intercept:表示是否计算截距,布尔型,默认为True,
# 若参数值为True时,代表训练模型需要加一个截距项;
# 若参数为False时,代表模型无需加截距项。
# normalize:布尔型,默认为False,若fit_intercept参数设置False时,normalize参数无需设置;
# 若normalize设置为True时,则输入的样本数据将( X - X均值) / | | X | |;
# 若设置normalize = False时,在训练模型前, 可以使用sklearn.preprocessing.StandardScaler进行标准化处理。
# copy_X,如果为True,则复制X
# n_jobs,并行任务时指定的CPU数量
# 属性:
# coef_:回归系数(斜率)
# intercept_:截距项
# 主要方法:
# fit(X, y, sample_weight=None) 训练模型
# predict(X) 用模型进行预测
# score(X, y, sample_weight=None),返回预测得分
# 其结果等于1 - (((y_true - y_pred) ** 2).sum() / ((y_true - y_true.mean()) ** 2).sum())
# score在-1范围内,越大预测性能越好
regr=linear_model.LinearRegression()
regr.fit(X_train,y_train)
coef=regr.coef_
intercept=regr.intercept_
trainscore=regr.score(X_train,y_train)
testscore=regr.score(X_test,y_test)
trainpredict=regr.predict(X_train)
testpredict=regr.predict(X_test)
meansquareerror=np.mean((regr.predict(X_test)-y_test)**2)
equalscore=np.mean(regr.predict(X_test)==y_test)
#print('Coefficients={},intercept={}'.format(coef,intercept))
## Coefficients=[ -43.26774487 -208.67053951 593.39797213 302.89814903 -560.27689824 261.47657106 -8.83343952 135.93715156 703.22658427 28.34844354]
## intercept=153.06798218266258
#print('Residual sum of squares={}'.format(meansquareerror))
## Residual sum of squares=3180.1988368427274
#print('trainscore={}'.format(trainscore))
## trainscore=0.555437148935302
#print('testscore={}'.format(testscore))
## testscore=0.35940090989715534
#print('equalscore={:.2f}'.format(equalscore))
## standardscore=0.00
#print('trainpredict={}'.format(trainpredict))
#print('testpredict={}'.format(testpredict))
# 岭回归
def test_Ridge_Regression(*data):
# lasso回归也是一种正则化的线性回归,且也是约束系数使其接近于,
# 不过其用到的方法不同,岭回归用到的是L2正则化,
# 而lasso回归用到的是L1正则化(L1是通过稀疏参数(减少参数的数量)来降低复杂度,即L1正则化使参数为零,L2是通过减小参数值的大小来降低复杂度,
# Parameters
# alpha:正则化系数,较大的值指定更强的正则化。
# fit_intercept:是否计算模型的截距,默认为True,计算截距
# normalize:在需要计算截距时,如果值为True,则变量x在进行回归之前先进行归一化(),如果需要进行标准化则normalize=False。若不计算截距,则忽略此参数。
# copy_X:默认为True,将复制X;否则,X可能在计算中被覆盖。
# max_iter:共轭梯度求解器的最大迭代次数。对于sparse_cg和lsqr,默认值由scipy.sparse.linalg确定。对于sag求解器,默认值为1000.
# tol:float类型,指定计算精度。
# solver:求解器{auto,svd,cholesky,lsqr,sparse_cg,sag,saga}
# aotu:根据数据类型自动选择求解器
# svd:使用X的奇异值分解计算岭系数。奇异矩阵比cholesky更稳定
# cholesky:使用标准的scipy.linalg.solve函数获得收敛的系数
# sparsr_cg:使用scipy.sparse.linalg.cg中的共轭梯度求解器。作为一种迭代算法,这个求解器比cholesky更适合大规模数据(设置tol和max_iter的可能性)
# lsqr:使用专用的正则化最小二乘方法scipy.sparse.linalg.lsqr。
# sag:使用随机平均梯度下降,saga使用其改进的,无偏见的版本,两种方法都使用迭代过程。
# random_state:随机数生成器的种子。
# Attributes
# coef_:返回模型的估计系数。
# intercept_:线性模型的独立项,一维情形下的截距。
# n_iter:实际迭代次数。
# Methods
# fit(X,y):使用数据训练模型
# get_params([deep=True]):返回函数LinearRegression()内部的参数值
# predict(X):使用模型做预测
# score(X,y):返回模型的拟合优度判定系数
# 为回归平方和与总离差平方和的比值,介于-1之间,越接近1模型的拟合效果越显著。
X_train, X_test, y_train, y_test = data
regr = linear_model.Ridge()
regr.fit(X_train,y_train)
coef = regr.coef_
intercept = regr.intercept_
trainscore = regr.score(X_train, y_train)
testscore = regr.score(X_test, y_test)
trainpredict = regr.predict(X_train)
testpredict = regr.predict(X_test)
meansquareerror = np.mean((regr.predict(X_test) - y_test) ** 2)
equalscore = np.mean(regr.predict(X_test) == y_test)
# print('Coefficients={},intercept={}'.format(coef,intercept))
# # Coefficients=[ 21.19927911 -60.47711393 302.87575204 179.41206395 8.90911449 -28.8080548 -149.30722541 112.67185758 250.53760873 99.57749017],intercept=152.4477761489962
# # intercept=3192.3285539937624
# print('Residual sum of squares={}'.format(meansquareerror))
# # Residual sum of squares=3192.3285539937624
# print('trainscore={}'.format(trainscore))
# # trainscore=0.4625439622495925
# print('testscore={}'.format(testscore))
# # testscore=0.35695757658096805
# print('equalscore={:.2f}'.format(equalscore))
# # standardscore=0.00
# print('trainpredict={}'.format(trainpredict))
# print('testpredict={}'.format(testpredict))
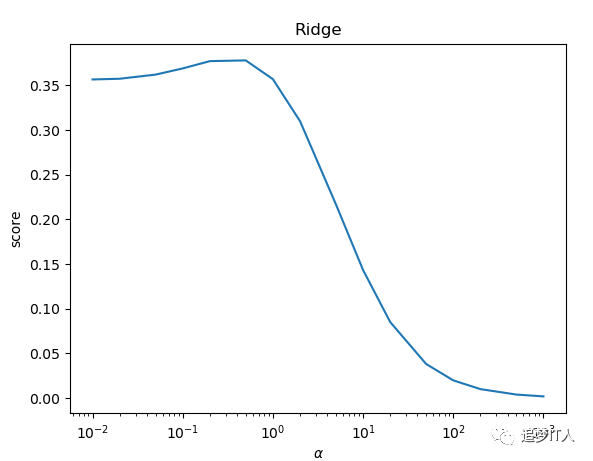
def test_Ridge_alpha(*data):
X_train, X_test, y_train, y_test = data
alphas=[0.01,0.02,0.05,0.1,0.2,0.5,1,2,5,10,20,50,100,200,500,1000]
scores=[]
for i,alpha in enumerate(alphas):
regr=linear_model.Ridge(alpha=alpha)
regr.fit(X_train,y_train)
scores.append(regr.score(X_test,y_test))
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
ax.plot(alphas,scores)
ax.set_xlabel(r'$\alpha$')
ax.set_ylabel(r'score')
ax.set_xscale('log')
ax.set_TItle('Ridge')
plt.show()
# Lasso回归
def test_Lasso_Regression(*data):
# 岭回归是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,
# 通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
# Parameters
# alpha : float, 可选,默认 1.0。当 alpha 为 时算法等同于普通最小二乘法
# fit_intercept : 是否计算模型的截距,默认为True,计算截距
# normalize : boolean, 可选, 默认 False; 若 True,则先 normalize 再 regression。若 fit_intercept 为 false 则忽略此参数。
# copy_X : 默认为True,将复制X;否则,X可能在计算中被覆盖。
# precompute : True | False | array-like, 默认=False
# max_iter : int, 可选,最大循环次数。
# tol : float, 可选,优化容忍度 The tolerance for the opTImization: 若更新后小于 tol,优化代码检查优化的 dual gap 并继续直到小于 tol 为止。
# warm_start : bool, 可选。为 True 时, 重复使用上一次学习作为初始化,否则直接清除上次方案。
# positive : bool, 可选。设为 True 时,强制使系数为正。
# selection : str, 默认 ‘cyclic’
# 若设为 ‘random’, 每次循环会随机更新参数,而按照默认设置则会依次更新。设为随机通常会极大地加速交点(convergence)的产生,尤其是 tol 比 1e-4 大的情况下。
# random_state : int, RandomState instance, 或者 None (默认值)
# Attributes
# coef_:返回模型的估计系数。
# intercept_:线性模型的独立项,一维情形下的截距。
# n_iter:实际迭代次数。
# Methods
# fit(X,y):使用数据训练模型
# get_params([deep=True]):返回函数LinearRegression()内部的参数值
# predict(X):使用模型做预测
# score(X,y):预测性能得分
# 为回归平方和与总离差平方和的比值,介于-1之间,越接近1模型的拟合效果越显著。
X_train, X_test, y_train, y_test = data
regr = linear_model.Lasso()
regr.fit(X_train, y_train)
coef = regr.coef_
intercept = regr.intercept_
trainscore = regr.score(X_train, y_train)
testscore = regr.score(X_test, y_test)
trainpredict = regr.predict(X_train)
testpredict = regr.predict(X_test)
meansquareerror = np.mean((regr.predict(X_test) - y_test) ** 2)
equalscore = np.mean(regr.predict(X_test) == y_test)
# print('Coefficients={},intercept={}'.format(coef,intercept))
# # Coefficients=[ 0. -0. 442.67992538 0. 0. 0. -0. 0. 330.76014648 0. ]
# # intercept=152.52260710501807
# print('Residual sum of squares={}'.format(meansquareerror))
# # Residual sum of squares=3583.4215227615487
# print('trainscore={}'.format(trainscore))
# # trainscore=0.41412544493966097
# print('testscore={}'.format(testscore))
# # testscore=0.27817828862078764
# print('equalscore={:.2f}'.format(equalscore))
# # standardscore=0.00
# print('trainpredict={}'.format(trainpredict))
# print('testpredict={}'.format(testpredict))
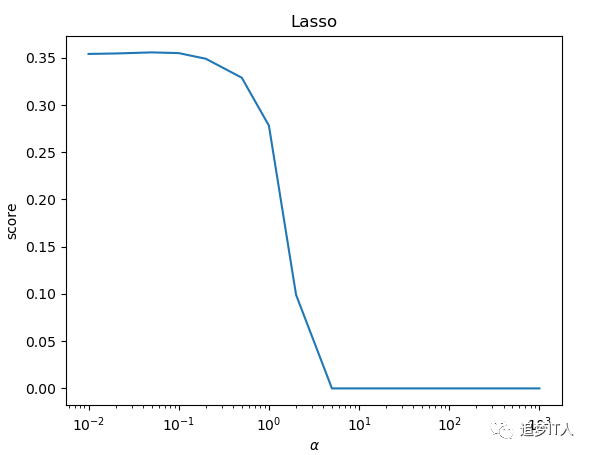
def test_Lasso_alpha(*data):
X_train, X_test, y_train, y_test = data
alphas = [0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000]
scores = []
for i, alpha in enumerate(alphas):
regr = linear_model.Lasso(alpha=alpha)
regr.fit(X_train, y_train)
scores.append(regr.score(X_test, y_test))
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(alphas, scores)
ax.set_xlabel(r'$\alpha$')
ax.set_ylabel(r'score')
ax.set_xscale('log')
ax.set_title('Lasso')
plt.show()
# ElasticNet回归
def test_ElasticNet_Regression(*data):
# ElasticNet回归是对Lasso回归和Ridge回归的融合,利用了L1和L2范数的融合,所以在参数中除了alpha之外还有L1_ratio 默认alpha=1,l1_ratio=0.5
# Parameters
# alpha: a值。
# fit_intercept:一个布尔值,指定是否需要计算b值。如果为False,那么不计算b值(模型会认为你已经将数据中心化了)。
# max_iter:整数值,指定最大迭代次数。
# normalize:一个布尔值。如果为True,那么训练样本会在回归之前被归一化。
# copy_X:一个布尔值,如果为True,则会复制X值
# precompute:一个布尔值或者一个序列。他决定是否提前计算Gram矩阵来加速计算。
# tol:一个浮点数,指定判断迭代收敛与否的阈值。
# warm_start:一个布尔值,如为True,那么使用前一次训练结果继续训练。否则重头开始训练。
# positive:一个布尔值,如为Ture,那么强制要求全中响亮的分量都为整数。
# selection:一个字符串,可以为‘cyclic’(更新时候,从前向后一次选择权重向量的一个分量来更新)或者‘random'(随机选择权重向量的一个分量来更新),他指定了当每轮迭代的时候,选择权重向量的一个分量来更新
# random_state:一个整数或者一个RandomState实例,或者为None。
# Attributes
# coef_:返回模型的估计系数。
# intercept_:线性模型的独立项,一维情形下的截距。
# n_iter:实际迭代次数。
# Methods
# fit(X,y):使用数据训练模型
# get_params([deep=True]):返回函数LinearRegression()内部的参数值
# predict(X):使用模型做预测
# score(X,y):预测性能得分
# 为回归平方和与总离差平方和的比值,介于0-1之间,越接近1模型的拟合效果越显著。
X_train, X_test, y_train, y_test = data
regr = linear_model.ElasticNet()
regr.fit(X_train, y_train)
coef = regr.coef_
intercept = regr.intercept_
trainscore = regr.score(X_train, y_train)
testscore = regr.score(X_test, y_test)
trainpredict = regr.predict(X_train)
testpredict = regr.predict(X_test)
meansquareerror = np.mean((regr.predict(X_test) - y_test) ** 2)
equalscore = np.mean(regr.predict(X_test) == y_test)
# print('Coefficients={},intercept={}'.format(coef,intercept))
# # Coefficients=[ 0.40560736 0. 3.76542456 2.38531508 0.58677945 0.22891647 -2.15858149 2.33867566 3.49846121 1.98299707],intercept=151.92763641451165
# # intercept=151.92763641451165
# print('Residual sum of squares={}'.format(meansquareerror))
# # Residual sum of squares=4922.355075721768
# print('trainscore={}'.format(trainscore))
# # trainscore=0.010304451830727368
# print('testscore={}'.format(testscore))
# # testscore=0.008472003027015784
# print('equalscore={:.2f}'.format(equalscore))
# # standardscore=0.00
# print('trainpredict={}'.format(trainpredict))
# print('testpredict={}'.format(testpredict))
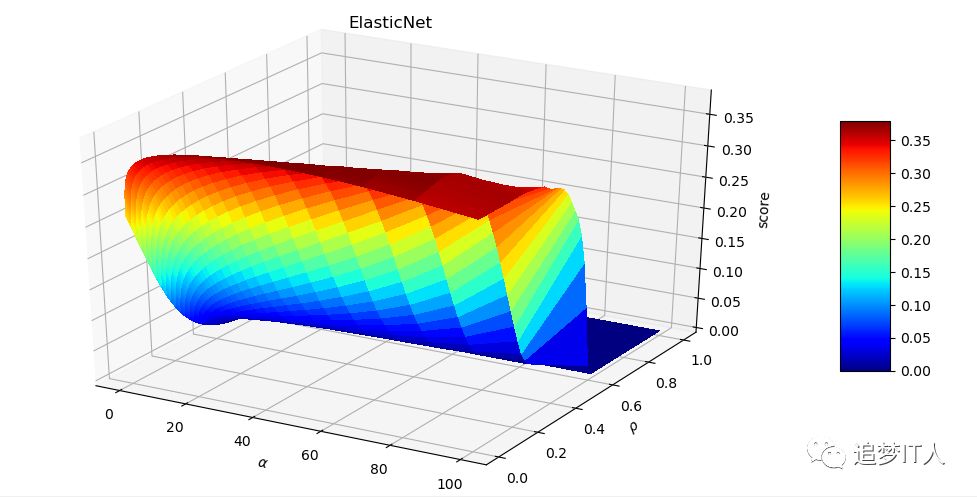
def test_ElasticNet_alpha_rho(*data):
X_train, X_test, y_train, y_test = data
alphas = np.logspace(-2,2) #log分布间距生成list
rhos=np.linspace(0.01,1) #取线性,均匀返回五是个值
scores = []
for alpha in alphas:
for rho in rhos:
regr = linear_model.ElasticNet(alpha=alpha,l1_ratio=rho)
regr.fit(X_train, y_train)
scores.append(regr.score(X_test, y_test))
# 绘图
alphas,rhos=np.meshgrid(alphas,rhos)
scores=np.array(scores).reshape(alphas.shape)
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = plt.figure(figsize=(10,5))
ax=Axes3D(fig)
surf=ax.plot_surface(alphas,rhos,scores,rstride=1,cstride=1,cmap=cm.jet,linewidth=0,antialiased=False)
fig.colorbar(surf,shrink=0.5,aspect=5)
ax.set_xlabel(r'$\alpha$')
ax.set_ylabel(r'$\rho$')
ax.set_zlabel('score')
ax.set_title('ElasticNet')
plt.show()
# 加载鸢尾花数据
def load_iris_data():
iris=datasets.load_iris()
X_train=iris.data
y_train=iris.target
return model_selection.train_test_split(X_train,y_train,test_size=0.25,random_state=0,stratify=y_train)
# 逻辑回归
def test_Logistic_Regression(*data):
# logistic 回归,虽然名字里有 “回归” 二字,但实际上是解决分类问题的一类线性模型。
# maximum-entropy classification(MaxEnt,最大熵分类),或 log-linear classifier(对数线性分类器)。
# 该模型利用函数 logistic function 将单次试验(single trial)的可能结果输出为概率。
# scikit-learn 中 logistic 回归在 LogisticRegression 类中实现了二分类(binary)、一对多分类(one-vs-rest)及多项式 logistic 回归,并带有可选的 L1 和 L2 正则化。
# Parameters
# penalty='l2' : 字符串‘l1’或‘l2’,默认‘l2’。
# 用来指定惩罚的基准(正则化参数)。只有‘l2’支持‘newton-cg’、‘sag’和‘lbfgs’这三种算法。
# 如果选择‘l2’,solver参数可以选择‘liblinear’、‘newton-cg’、‘sag’和‘lbfgs’这四种算法;如果选择‘l1’的话就只能用‘liblinear’算法。
# dual=False : 对偶或者原始方法。Dual只适用于正则化相为l2的‘liblinear’的情况,通常样本数大于特征数的情况下,默认为False。
# C=1.0 : C为正则化系数λ的倒数,必须为正数,默认为1。和SVM中的C一样,值越小,代表正则化越强。
# fit_intercept=True : 是否存在截距,默认存在。
# intercept_scaling=1 : 仅在正则化项为‘liblinear’,且fit_intercept设置为True时有用。
# solver='liblinear' : solver参数决定了我们对逻辑回归损失函数的优化方法,有四种算法可以选择。
# a) liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
# b) lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
# c) newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
# d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
# multi_class='ovr' : 分类方式。
# ovr即one-vs-rest(OvR),multinomial是many-vs-many(MvM)。
# 如果是二元逻辑回归,ovr和multinomial并没有任何区别,区别主要在多元逻辑回归上。
# ovr不论是几元回归,都当成二元回归来处理。mvm从从多个类中每次选两个类进行二元回归。如果总共有T类,需要T(T-1)/2次分类。
# OvR相对简单,但分类效果相对略差(大多数样本分布情况)。而MvM分类相对精确,但是分类速度没有OvR快。
# 如果选择了ovr,则4种损失函数的优化方法liblinear,newton-cg,lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了。
# class_weight=None : 类型权重参数。用于标示分类模型中各种类型的权重。默认不输入,即所有的分类的权重一样。
# 选择‘balanced’自动根据y值计算类型权重。
# 自己设置权重,格式:{class_label: weight}。例如0,1分类的er'yuan二元模型,设置class_weight={:0.9, 1:0.1},这样类型的权重为90%,而类型1的权重为10%。
# random_state=None : 随机数种子,默认为无。仅在正则化优化算法为sag,liblinear时有用。
# max_iter=100 : 算法收敛的最大迭代次数。
# tol=0.0001 : 迭代终止判据的误差范围。
# verbose= : 日志冗长度int:冗长度;:不输出训练过程;1:偶尔输出;>1:对每个子模型都输出
# warm_start=False : 是否热启动,如果是,则下一次训练是以追加树的形式进行(重新使用上一次的调用作为初始化)。布尔型,默认False。
# n_jobs=1 : 并行数,int:个数;-1:跟CPU核数一致;1:默认值。
# Attributes
# coef_:返回模型的估计系数。
# intercept_:线性模型的独立项,一维情形下的截距。
# n_iter:实际迭代次数。
# Methods
# fit(X, y, sample_weight=None)
# 拟合模型,用来训练LR分类器,其中X是训练样本,y是对应的标记向量
# 返回对象,self。
# fit_transform(X, y=None, **fit_params)
# fit与transform的结合,先fit后transform。返回X_new:numpy矩阵。
# predict(X)
# 用来预测样本,也就是分类,X是测试集。返回array。
# predict_proba(X)
# 输出分类概率。返回每种类别的概率,按照分类类别顺序给出。如果是多分类问题,multi_class="multinomial",则会给出样本对于每种类别的概率。
# 返回array-like。
# score(X, y, sample_weight=None)
# 返回给定测试集合的平均准确率(mean accuracy),浮点型数值。
# 对于多个分类返回,则返回每个类别的准确率组成的哈希矩阵。
X_train, X_test, y_train, y_test = data
regr = linear_model.LogisticRegression()
regr.fit(X_train, y_train)
coef = regr.coef_
intercept = regr.intercept_
trainscore = regr.score(X_train, y_train)
testscore = regr.score(X_test, y_test)
trainpredict = regr.predict(X_train)
testpredict = regr.predict(X_test)
meansquareerror = np.mean((regr.predict(X_test) - y_test) ** 2)
equalscore = np.mean(regr.predict(X_test) == y_test)
# print('Coefficients={},intercept={}'.format(coef,intercept))
# # Coefficients=[[-0.38340846 0.86187824 -2.27003634 -0.9744431 ]
# # [ 0.34360292 -0.37876116 -0.03099424 -0.86880637]
# # [ 0.03980554 -0.48311708 2.30103059 1.84324947]]
# # intercept=[ 8.75830949 2.49431233 -11.25262182]
# print('Residual sum of squares={}'.format(meansquareerror))
# # Residual sum of squares=0.0
# print('trainscore={:.2f}'.format(trainscore))
# # trainscore=0.9553571428571429
# print('testscore={:.2f}'.format(testscore))
# # testscore=1.0
# print('equalscore={:.2f}'.format(equalscore))
# # standardscore=1.00
# print('trainpredict={}'.format(trainpredict))
# print('testpredict={}'.format(testpredict))
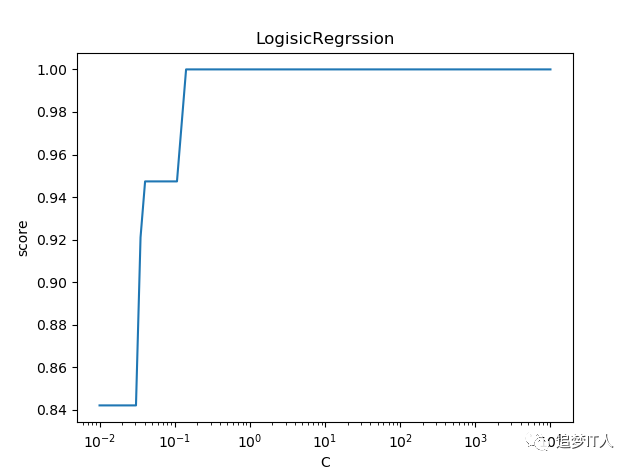
def test_Logistic_Regression_C(*data):
X_train, X_test, y_train, y_test = data
Cs=np.logspace(-2,4,num=100)
scores = []
for C in Cs:
regr = linear_model.LogisticRegression(C=C)
regr.fit(X_train, y_train)
scores.append(regr.score(X_test, y_test))
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(Cs, scores)
ax.set_xlabel(r'C')
ax.set_ylabel(r'score')
ax.set_xscale('log')
ax.set_title('LogisicRegrssion')
plt.show()
# 线性判别分析回归
def test_LDA(*data):
# ElasticNet回归是对Lasso回归和Ridge回归的融合,利用了L1和L2范数的融合,所以在参数中除了alpha之外还有L1_ratio 默认alpha=1,l1_ratio=0.5
# Parameters
# solver:一个字符串,指定了求解最优化问题的算法,可以为如下的值。
# 'svd':奇异值分解。对于有大规模特征的数据,推荐用这种算法。
# 'lsqr':最小平方差,可以结合skrinkage参数。
# 'eigen' :特征分解算法,可以结合shrinkage参数。
# skrinkage:字符串‘auto’或者浮点数活者None。该参数通常在训练样本数量小于特征数量的场合下使用。该参数只有在solver=lsqr或者eigen下才有意义
# '字符串‘auto’:根据Ledoit-Wolf引理来自动决定shrinkage参数的大小。
# 'None:不使用shrinkage参数。
# 浮点数(位于~1之间):指定shrinkage参数。
# priors:一个数组,数组中的元素依次指定了每个类别的先验概率。如果为None,则认为每个类的先验概率都是等可能的。
# n_components:一个整数。指定了数组降维后的维度(该值必须小于n_classes-1)。
# store_covariance:一个布尔值。如果为True,则需要额外计算每个类别的协方差矩阵。
# warm_start:一个布尔值。如果为True,那么使用前一次训练结果继续训练,否则从头开始训练。
# tol:一个浮点数。它指定了用于SVD算法中评判迭代收敛的阈值。
# ————————————————
# Attributes
# coef_:权重向量。
# intercept:b值。
# covariance_:一个数组,依次给出了每个类别烦人协方差矩阵。
# means_:一个数组,依次给出了每个类别的均值向量。
# xbar_:给出了整体样本的均值向量。
# n_iter_:实际迭代次数。
# Methods
# fix(X,y):训练模型。
# predict(X):用模型进行预测,返回预测值。
# score(X,y[,sample_weight]):返回(X,y)上的预测准确率(accuracy)。
# predict_log_proba(X):返回一个数组,数组的元素一次是 X 预测为各个类别的概率的对数值。
# predict_proba(X):返回一个数组,数组元素一次是 X 预测为各个类别的概率的概率值。
X_train, X_test, y_train, y_test = data
lda = discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(X_train, y_train)
coef = lda.coef_
intercept = lda.intercept_
trainscore = lda.score(X_train, y_train)
testscore = lda.score(X_test, y_test)
trainpredict = lda.predict(X_train)
testpredict = lda.predict(X_test)
meansquareerror = np.mean((lda.predict(X_test) - y_test) ** 2)
equalscore = np.mean(lda.predict(X_test) == y_test)
# print('Coefficients={},intercept={}'.format(coef,intercept))
# # Coefficients=[[ 6.66775427 9.63817442 -14.4828516 -20.9501241 ][ -2.00416487 -3.51569814 4.27687513 2.44146469][ -4.54086336 -5.96135848 9.93739814 18.02158943]]
# # intercept=[-15.46769144 0.60345075 -30.41543234]
# print('Residual sum of squares={}'.format(meansquareerror))
# # Residual sum of squares=0.9
# print('trainscore={}'.format(trainscore))
# # trainscore=0.9732142857142857
# print('testscore={}'.format(testscore))
# # testscore=1.0
# print('equalscore={:.2f}'.format(equalscore))
# # equalscore=0.00
# print('trainpredict={}'.format(trainpredict))
# print('testpredict={}'.format(testpredict))
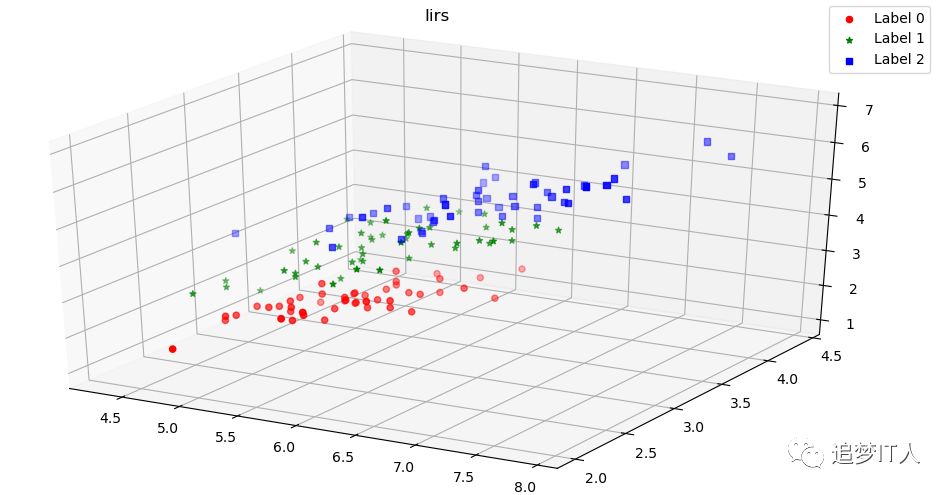
def plot_LDA(converted_X,y):
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure(figsize=(10,5))
ax=Axes3D(fig)
colors='rgb'
markers='o*s'
for target,color,marker in zip([,1,2],colors,markers):
pos=(y==target).ravel()
X=converted_X[pos,:]
ax.scatter(X[:,],X[:,1],X[:,2],color=color,marker=marker,label='Label %d'%target)
ax.legend(loc='best')
fig.suptitle('Iirs')
plt.show()
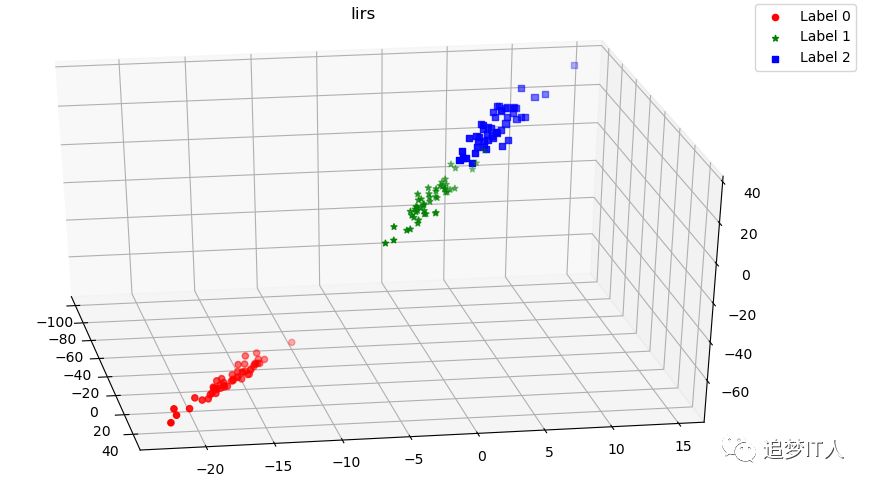
def plot_LDA_diff(*data):
X_train, X_test, y_train, y_test = data
X=np.vstack((X_train,X_test))
Y=np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))
plot_LDA(X,Y)
lda=discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(X,Y)
convertedX=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
plot_LDA(convertedX,Y)
def f(x):
randa = np.random.uniform(, 0.5, size=x.shape)
randb = np.random.uniform(, 2, size=x.shape)
randc = np.random.uniform(, 2, size=x.shape)
return x*x*(randa+1)-x*(randb+2)-randc
def load_ploy_data():
X=np.linspace(1,100,100)
y = f(X)
c = list(zip(X, y))
np.random.shuffle(c)
newX,newy=zip(*c)
size=20
newX=list(newX)
newy=list(newy)
X_train=np.array(newX[:size])
y_train=np.array(newy[:size])
X_test=np.array(newX[size:])
y_test=np.array(newy[size:])
X = X[:, np.newaxis]
X_train = X_train[:, np.newaxis]
y_train = y_train[:, np.newaxis]
X_test = X_test[:, np.newaxis]
y_test = y_test[:, np.newaxis]
return X_train, X_test, y_train, y_test,X,y
def test_PolynomialFeatures(degree,*data):
# 机器学习中一种常见的模式,是使用线性模型训练数据的非线性函数。
# 这种方法保持了一般快速的线性方法的性能,同时允许它们适应更广泛的数据范围。
# 主要参数
# degree:控制多项式的度
# interaction_only:默认为False,如果指定为True,那么就不会有特征自己和自己结合的项,上面的二次项中没有a^2和b^2。
# include_bias:默认为True。如果为True的话,那么就会有上面的 1那一项。
X_train, X_test, y_train, y_test = data
model = Pipeline([('poly', preprocessing.PolynomialFeatures(degree=degree)),
('linear', linear_model.LinearRegression())])
model.fit(X_train,y_train)
X=np.vstack((X_train,X_test))
coef = model.named_steps['linear'].coef_
intercept = model.named_steps['linear'].intercept_
y_plot = model.predict(X)
print('Coefficients={},intercept={}'.format(coef, intercept))
# Coefficients=[-6.52563764e-09 4.07601927e+01 -2.10719706e+02 5.42901460e+02...]
# intercept=intercept=188.12644759943421
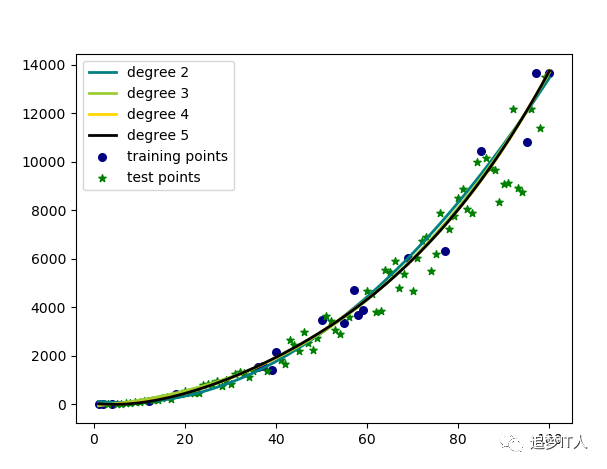
def test_PolynomialFeatures_degree(*data):
X_train, X_test, y_train, y_test,X,y = data
plt.scatter(X_train,y_train, color='navy', s=30, marker='o', label="training points")
plt.scatter(X_test, y_test, color='green', s=30, marker='*', label="test points")
colors = ['teal', 'yellowgreen', 'gold','black']
for count, degree in enumerate([2 ,3, 4, 5]):
model = Pipeline([('poly', preprocessing.PolynomialFeatures(degree=degree)),
('linear', linear_model.LinearRegression())])
model.fit(X_train,y_train)
y_plot=model.predict(X)
plt.plot(X, y_plot, color=colors[count], linewidth=2,label="degree %d" % degree)
plt.legend()
plt.show()
if __name__ == '__main__':
X_train,X_test,y_train,y_test=load_data()
test_LinearRegression(X_train,X_test,y_train,y_test)
test_Ridge_Regression(X_train,X_test,y_train,y_test)
test_Ridge_alpha(X_train,X_test,y_train,y_test)
test_Lasso_Regression(X_train,X_test,y_train,y_test)
test_Lasso_alpha(X_train,X_test,y_train,y_test)
test_ElasticNet_Regression(X_train,X_test,y_train,y_test)
test_ElasticNet_alpha_rho(X_train,X_test,y_train,y_test)
X_train, X_test, y_train, y_test = load_iris_data()
test_Logistic_Regression(X_train,X_test,y_train,y_test)
test_Logistic_Regression_C(X_train,X_test,y_train,y_test)
test_LDA(X_train,X_test,y_train,y_test)
plot_LDA_diff(X_train,X_test,y_train,y_test)
X_train, X_test, y_train, y_test,X,y = load_ploy_data()
test_PolynomialFeatures(2,X_train,X_test,y_train,y_test)
test_PolynomialFeatures_degree(X_train,X_test,y_train,y_test,X,y)
# 线性判别分析回归
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)