最大限度地减少组件的变化敏感性的单运算放大器滤波器-Mini

Abstract: By delving a little more deeply into the Sallen-Key filter's component sensiTIviTIes, we discover a "sweet spot" in the mathemaTIcal analysis that allows the design of simple, single op amp filters whose performance rivals that of more complicated filters. This approach has been useful in extending the uTIlity of Sallen-Key filters.



Dozens of filter topologies have been devised over the years, each with its own advantages. Yet engineers often rely on a small but popular subgroup of those topologies for which "cookbook" design methods are available. They choose simpler, single-op-amp filters for the less complicated lower-order designs. But when the associated cookbook approaches fail in developing a well-behaved complex filter, engineers generally turn to more complicated topologies. However, a deeper analysis of a common single-op-amp topology (the Sallen-Key filter) can lead to some interesting results if you dig below the level of cookbook formulas.

A typical filter-design process has three main stages. First, you establish the frequency range to be passed, the allowable passband ripple, etc., as determined by the system requirements. Next, you determine a transfer function (mathematical filter description) that meets the requirements, usually by choosing one of the standard types: Butterworth, Chebyshev, Bessel, Elliptical, etc. This step in the process is beyond the scope of the present article, but detailed information can be obtained from the references listed at the end.

The final step is to design and implement a circuit that provides the desired transfer function. The designer typically follows a strategy similar to the following, which is quite simple when applied to the cookbook topologies:

• Factor the transfer function into second-order parts.
• Choose a circuit topology (or topologies) that allows each second-order function to be synthesized independently.
• Design each stage as an independent second-order filter.
• Connect the resulting second-order filters in series.

A limitation common to the cookbook approaches can arise at this point. Single-op-amp filters often exhibit great sensitivity to variations in their passive-component values, and filters with high Qs (i.e., most higher-order filters) are particularly sensitive. This sensitivity would not be a problem with perfect passive components, but actual components are available only in a limited number of standard values. Cookbook calculations can call for a 10.095k resistor, yet the nearest value actually available might be 10.0k.

Real-component values also vary from unit to unit and in response to variations in temperature and other environmental factors. The filter's sensitivity to these component variations can cause it to deviate significantly from its desired frequency response. In many cases, the designer then turns to a more complicated filter topology. The Sallen-Key TopologyThe Sallen-Key filter (Reference 1) is among the most common single-op-amp filters. Its low-pass version (Figure 1) has these design equations:

where ωn is the natural frequency, Q is the "quality factor" (a measure of the peaking that occurs near the natural frequency), and K = 1 + RB/RA is the DC gain.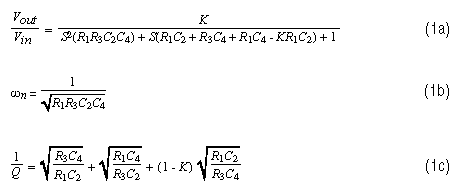


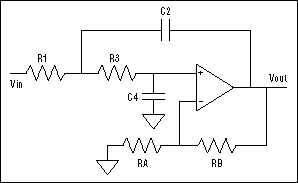
Figure 1. Filter Sensitivity to Component VariationsNatural-frequency and Q sensitivities are useful for evaluating transfer-function stability. For the Sallen-Key filter (given in Reference 2 on page 159), these sensitivities are as follows:

Sensitivity is represented by 'S'. Its superscript is the circuit characteristic whose sensitivity is being evaluated, and its subscript is the circuit element whose effect on that characteristic is being evaluated. Thus, the first sensitivity equation (2a) shows the sensitivity of Q to variations in R1 or R3.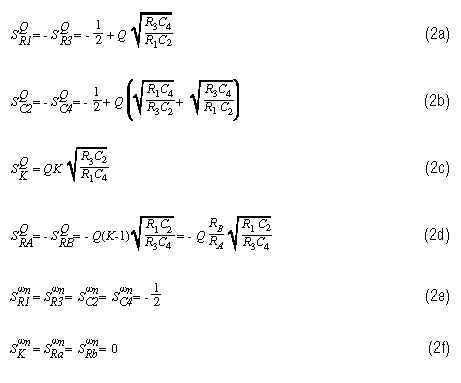

S is the power to which a component variation is raised to calculate the corresponding variation in a circuit characteristic. You may have noticed, for example, that the power for all the natural-frequency sensitivities is either -1/2 or 0. When S = -1/2 and the component varies by a factor of 'A', the natural frequency varies by A-0.5 (i.e., 1/√A). Thus, the new natural frequency will be the original frequency divided by √A. When S = 0, the frequency does not change, because A0 = 1.

Reference 2 covers sensitivity in much greater detail, and it includes the derivations of many of the sensitivity equations listed above. References 3 and 4 also have good treatments of this important subject. These equations are so complicated that it often is quite difficult to choose the six passive components for a desired natural frequency and Q, while simultaneously achieving low-Q sensitivities, unless you play around with the equations and notice some interesting things that happen when the gain (K) is set to 1. K = 1 Simplifies the Sallen-Key FilterWe can simplify the Sallen-Key filter equations a great deal by choosing K = 1 as the DC gain value. In this case, the equation for Q (equation 1c) simplifies to

We also find that the sensitivity of Q to RA and RB goes to zero for K = 1 (equation 2d). This is no surprise. Setting K = 1 configures the op amp as a voltage follower by connecting its output directly to the inverting input, which eliminates RA and RB.

Substituting the simplified equation for Q (equation 3) into the sensitivity equations 2a and 2c simplifies those equations:

The sensitivity of Q to the resistors can be simplified further by setting the resistor values equal. When R1 and R3 are exactly equal, the sensitivity is zero. But the values of actual resistors are never truly equal. As they deviate from their nominal values, the sensitivity becomes non-zero but remains very small. Resistors with 5% tolerance, for example, cause a worst-case sensitivity of

Thus, 5% resistor variations produce a 0.12% Q variation, which is negligible in comparison to the other sensitivities. Even if the resistor values are not equal, this sensitivity is between -1/2 and +1/2. A closer look at the Q equation shows other reasons for setting R1 = R3:

When n = 1 (i.e., when R3 = R1), the quantity (n+1/n) has a minimum value of 2. Thus, the filter capacitors will be equal-valued when Q = 1/2 and the resistors are set equal to each other. For all Qs higher than 1/2 (the most common case by far), C2 must be larger than C4. If the resistors are not equal, the ratio of C2 to C4 must be made larger. To minimize this spread in capacitor values, the resistor values should therefore be equal.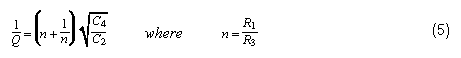

For equal resistor values, the equation for Q simplifies to

Rearranging this equation to get C2 in terms of C4,

We can substitute this expression into the equation for n (equation 1b) and solve for C4:

Substituting this result into the equation for C2 (equation 7), we get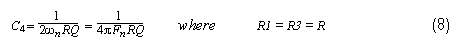

The Simplified Design ProcessSetting the Sallen-Key filter gain to unity and setting R1 = R3 enables the design of low-sensitivity single-op-amp filters by solving two simple equations. The simplified design process is as follows:

• Select an appropriate resistor value.
• Use equations 8 and 9 for solving the capacitor values.
• If C2 is too large, start over with a larger resistor value.
• If C4 is too small, start over with a smaller resistor value.
• If C4 is too small and C2 is too large, you have reached the limit for this filter.
• Pick standard values closest to the calculated values.

Two examples illustrate this method and the benefits derived from its use. Comparing the New Approach to a Cookbook ApproachThe first example comes from work done by the author several years ago. To minimize circuit variations in production, he redesigned a circuit (initially created with cookbook techniques) to realize a third-order Butterworth low-pass filter with a -3dB frequency of 4.8kHz. The redesign eliminated a trim pot and its associated need for tweaking.

This filter required a second-order stage with Q = 1 and a natural frequency of 4.8kHz. It was implemented initially with the Sallen-Key topology and the design approach of Reference 2, pages 156 to 157, which sets the resistor values equal (R1 = R3 = R) and capacitor values equal (C2 = C4 = C). Choosing C = 0.001µF resulted in gain (K) = 2 and R = 33.2K. The Q sensitivities for this circuit are as follows:

The filter was redesigned with our new method using the same resistor value (33.2kΩ). Equations 8 and 9 result in C2 = 2000pF and C4 = 500pf. The sensitivities are as follows: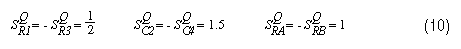

Figure 2 shows the schematics used to simulate these circuits, and Figure 3 the results of SPICE simulations. These frequency response plots are the result of a Monte Carlo run of 100 different "builds" for each filter, using 1%-tolerance resistors and 5% capacitors. For each "build," the SPICE simulator randomly varies the component values within their specified tolerances. Note that for all frequencies in the passband (especially those near the natural frequency), the new filter has substantially less variation than the old one.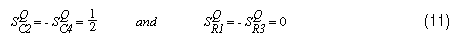


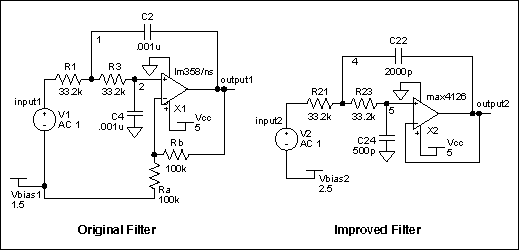
Figure 2.


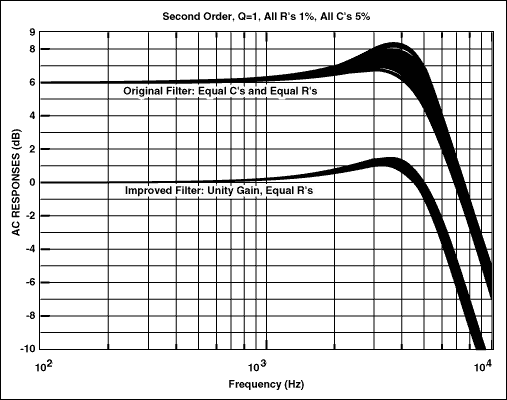
Figure 3.

It is also important to note that these simulation results are not the only steps needed to prove circuit operation; you should also build and test the circuit. Once the SPICE simulator indicates AC performance equal to that of the actual circuit with nominal component values, you can use the Monte Carlo function common in SPICE simulators to evaluate how the circuit response changes with variation in the components. Cascaded Stages Implement Higher-Order FiltersThe unity-gain Sallen-Key approach has two disadvantages. It cannot provide gain, and for high-Q filters its capacitor ratio may be too large to allow realization of the filter. Existing amplifier stages can often provide the needed gain; but, if not, the worst-case solution is to add a single-op-amp gain stage.

High-order filters often require at least one stage with a very high Q. This stage can be implemented with a more complicated topology, whereas the other stages are implemented with low-sensitivity Sallen-Key circuits. Even with Q limitations, the Sallen-Key topology can execute the high-order filters traditionally implemented with multi-op-amp topologies. The following example shows a new procedure for designing such a filter, demonstrating a dramatic improvement in performance over the older methods. Nominal specifications are as follows:

• Seventh-order Chebyshev
• 0.05dB ripple
• 8kHz -3dB frequency
• Gain = 10

An actual derivation of the transfer function from these objective specifications is beyond the scope of this article, but the references cover that subject in detail. The transfer function has three complex-pole pairs and one simple pole:

Fn