反相运算放大器基础知识讲解

　　运算放大器的开环增益（Avo）可能非常高，高达1000000（120dB）或更高。但是，这种非常高的增益对我们来说并没有实际用处，因为它使放大器既不稳定又难以控制，因为最小的输入信号，仅几个微伏（μV）就足以使输出电压达到饱和并向一个或另一个供电轨摆动，从而失去对输出的完全控制。

　　由于运算放大器的开环直流增益非常高，因此我们可以通过在放大器的输出端与反向输入端之间连接一个合适的电阻来降低和控制总增益，从而损失掉部分高增益放大器的 然后，这产生了通常称为负反馈的效果，因此产生了一个非常稳定的基于运算放大器的系统。

　　负反馈是将一部分输出信号“反馈”回输入的过程，但是要使反馈为负，我们必须使用外部将其反馈到运算放大器的负或“反相输入”端子。反馈电阻称为Rf。输出和反相输入端子之间的这种反馈连接迫使差分输入电压趋于零。

　　这种效应为放大器产生了一个闭环电路，导致放大器的增益为闭环增益。然后，闭环反相放大器使用负反馈来精确控制放大器的整体增益，但它是以降低放大器增益为代价的。

　　这种负反馈会导致反相输入端子上的信号与实际输入电压不同，因为它将是输入电压与负反馈电压之和，从而给它加上了求和点或总和项。因此，我们必须通过使用分开的反相输入端的真实输入信号输入电阻器。

　　由于我们没有使用正向同相输入，因此将其连接到公共接地或零电压端子，如下所示，但是这种闭环反馈电路的作用导致反相输入端的电势等于交流输入端的电势。同相输入产生一个虚拟接地求和点，因为它的电位与接地参考输入相同。换句话说，运算放大器变成了“差分放大器”。

　　反相运算放大器电路

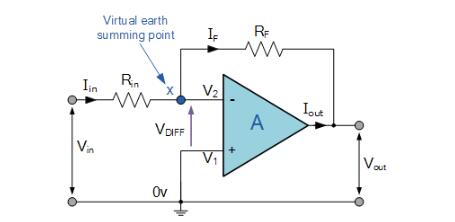
　　在此反相放大器电路中，运算放大器与反馈相连，以产生闭环 *** 作。在处理运算放大器时，要记住两个非常重要的反相放大器规则：“无电流流入输入端子”和“ V1始终等于V2”。但是，在实际的运算放大器电路中，这两个规则都被稍微打破了。

　　这是因为输入和反馈信号（X ）的结点 与正（+ ）输入的电位相同， 后者为零伏或接地，因此该结点是“虚拟接地”。由于存在这个虚拟接地节点，因此放大器的输入电阻等于输入电阻的值Rin，并且反相放大器的闭环增益可以通过两个外部电阻的比值来设置。

　　上面我们说过，关于反相放大器或与此相关的任何运算放大器，要记住两个非常重要的规则。

　　（1）无电流流入输入端子。

　　（2）当V1 = V2 = 0时，差分输入电压为零（虚拟接地）。

　　然后，通过使用这两个规则，我们可以使用第一原理导出用于计算反相放大器的闭环增益的方程式。

　　如图所示，电流（i）流经电阻器网络。

　　等式中的负号表示输出信号相对于输入反相，因为它的相位差为180 o。这是由于反馈的值为负。

　　输出电压Vout的等式还表明，对于固定的放大器增益，当Vout = Vin x Gain时，电路本质上是线性的。该属性对于将较小的传感器信号转换为较大的电压非常有用。

　　反相放大器的另一个有用应用是“跨阻放大器”电路。甲跨阻放大器也被称为“跨阻放大器”，基本上是（“in”和电压“出”电流）的电流-电压转换器。它们可用于低功率应用中，以将由光电二极管或光电检测设备等产生的很小电流转换成与输入电流成比例的可用输出电压，如图所示。

　　跨阻放大器电路

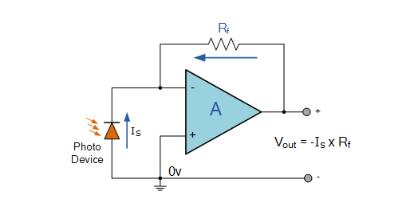
　　上面的简单光激活电路将光电二极管产生的电流转换为电压。反馈电阻Rf设置反相输入端的工作电压点并控制输出量。输出电压为Vout = I s xRf。因此，输出电压与光电二极管产生的输入电流成正比。

　　反相运算放大器示例1：

　　以下为反相放大器电路的闭环增益。

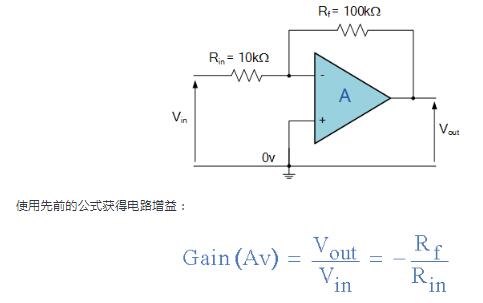
　　我们现在可以如下替换电路中电阻的值，

　　Rin =10kΩ 和 Rf=100kΩ

　　电路的增益计算为：-Rf/ Rin = 100k / 10k = -10

　　因此，上述反相放大器电路的闭环增益为-10或20dB（20log（10））。

　　反相运算放大器示例2：

　　将原始电路的增益增加到40（32dB），找到所需电阻的新值。

　　假设输入电阻保持在10KΩ的相同值，那么通过重新安排闭环电压增益公式，我们可以找到反馈电阻Rf所需的新值。

　　增益=Rf/ Rin

　　因此，Rf=增益x Rin

　　Rf= 40 x 10000

　　Rf= 400000或400KΩ

　　该电路的增益为40所需的新电阻值为：Rin =10KΩ 和 Rf=400KΩ。

　　我们还可以重新安排公式以提供新的Rin值，并保持Rf的值不变。

　　关于运算放大器的反相放大器配置，需要注意的最后一点是，如果两个电阻的值相等，Rin =Rf，则放大器的增益将为-1，从而在其输出上产生互补形式的输入电压，即Vout = -Vin。这种类型的反相放大器配置通常称为简单的反相缓冲器的单位增益反相器。