IQ正交调制及星座图

　　一个信号有三个特性随时间变化：幅度、相位或频率。然而，相位和频率仅仅是从不同的角度去观察或测量同一信号的变化。人们可以同时进行幅度和相位的调制，也可以分开进行调制，但是这既难于产生更难于检测。但是在特制的系统中信号可以分解为一组相对独立的分量：同相(I)和正交(Q)分量。这两个分量是正交的，且互不相干的。

　　正交幅度调制(QAM，Quadrature Amplitude ModulaTIon)是一种在两个正交载波上进行幅度调制的调制方式。这两个载波通常是相位差为90度(π/2)的正弦波，因此被称作正交载波。这种调制方式因此而得名。

　　图1中的QAM调制器中I和Q信号来自一个信号源，幅度和频率都相同，唯一不同的是Q信号的相位与I信号相差90o。具体关系如下图所示，当I的幅度为1的时候，Q的幅度为0，而当I的幅度为0的时候，Q的幅度为1，两个信号互不相干，相位相差90o，是正交的。

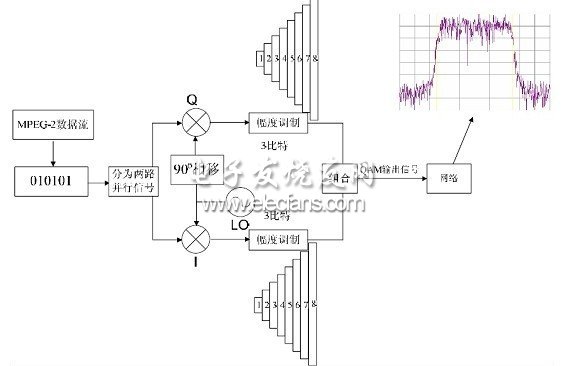
　　模拟信号的相位调制和数字信号的PSK可以被认为是幅度不变、仅有相位变化的特殊的正交幅度调制。由此，模拟信号频率调制和数字信号FSK也可以被认为是QAM的特例，因为它们本质上就是相位调制。

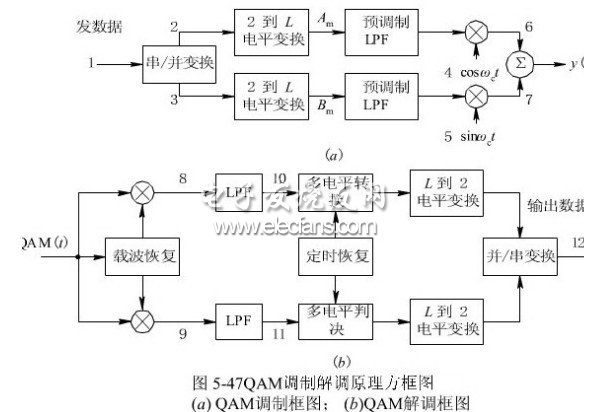
　　I-Q的调变信号可由同相载波和90度相移的载波相加合成，在电路上下直接牵涉到载波相位的改变，所以比较好实现。其次，通常I-Q图上只有几个固定点，简单的数字电路就足以腾任编码的工作。而且不同调变技术的差异只在于I-Q图上点的分布不同而已，所以只要改变I-Q编码器，利用同样的调变器，便可得到不同的调变结果。

　　I-Q解调变换的过程也很容易，只要取得和发射机相同的载波信号，解调器的方块图基本上只是调变器的反向而已。从硬件的开点而言，调变器和解调器的方块图上，没有会因为I-Q值的不同(不同的I-Q调变技术)而必须改变的部份，所以这两个方块图可以应用在所有的I-Q调变技术中。