利用电路的自然响应说明极点零点位置的影响

在我的学术生涯中，我注意到系统理论是最难教和最难学的课程之一。这些极点和零点概念在课堂上都感觉很有意思，但是一旦学生想将它们与实验室中的物理电路联系起来，理论和实践之间就会出现鸿沟。在这篇文章中，我将尝试找出关于极点和零点的物理感觉，使用运算放大器来控制它们在复平面中的位置，并利用电路的自然响应来说明极点/零点位置的影响。

单端口电路的自然响应

我们来看图1中的无源线性单端口电路，它包括电阻、电容和电感。

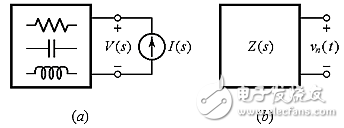
图1：（a）无源单端口电路 （b）自然（或无源）开路响应vn(t)。

如果我们施加一个测试电流I(s)，单端口电路将产生电压V(s)，使得V(s)=Z(s)/(s)，其中I(s)和V(s)是所施加电流和所产生电压的拉普拉斯变换，s是以sec-1为单位的复数频率。阻抗Z(s)是s的有理函数形式，即分子多项式N(s)与分母多项式D(s)的比值：

公式N(s)=0的根被称为Z(s)的零点，表示为z1，z2，……；而公式D(s)=0的根被称为Z(s)的极点，表示为p1、p2、……。极点和零点统称为根，也称为临界频率。例如，阻抗：

当s=0时，其值为零；当s=-3±j4时，它具有复共轭极点对。可以用根来表达它，即：

如果我们绘制|Z(s)|相对于s的幅度曲线，则可以直观理解零点和极点的含义。所得到的曲线就好像在s平面上竖起的帐篷，在零点处接触s平面，而在极点处其高度变为无限。

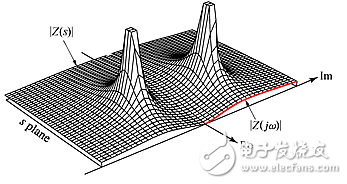
图2：Z(s)=(10Ω)s/(s2+6s+25)的幅度图。（通过在虚轴上计算|Z|获得的分布曲线图显示出单端口电路的交流响应。）

为了找到极点的物理感觉，我们在s接近极点pk时施加电流I(s)，就可以用相当小的I(s)获得给定的电压V(s)。s越接近极点pk，获得给定电压V(s)所需的电流I(s)越小。在s→pk的极限状态下，即使电流为零，即开路，单端口电路也会获得一个非零的供电电压（见图1b）！这个电压称为自然响应或无源响应，因为单端口电路可利用储存在其电容和电感内部的能量来产生电压。这些能量在电阻中消耗尽了，在无源单端口的情况下，它们将随时间呈指数级衰减。实际上，系统理论预测到自然响应符合以下表达式：

其中a1，a2，......，是取决于存储能量的合适系数（以V为单位），Z(s)的极点是指数中时间常数的倒数。

那么Z(s)的零点呢？我们来看图3，它表示图1的两种情况。现在施加的信号是电压V(s)，而响应是电流I(s)=[1/Z(s)]V(s)，这表明Z(s)的零点现在成为1/Z(s)的极点。通过双重推理，在s→zk的极限状态下，即使施加零电压（短路），单端口电路也将提供非零电流（参见图3b）！该电流称为自然响应或无源响应，因为单端口电路利用储存在其电容和电感内部的能量来产生电流。系统理论预测自然短路电流响应符合以下表达式：

其中b1，b2，......，是取决于存储能量的合适系数（以安培为单位），Z(s)的零点是指数中时间常数的倒数。

图3：（a）无源单端口电路（b）自然（或无源）短路响应in(t)。

总而言之，单端口电路的自然响应由其阻抗Z(s)的根控制：极点控制开路电压响应vn(t)，而零点控制短路电流响应in(t)。在某种程度上，根就像是单端口电路的DNA。例如，我们来看图4的单端口电路。在t=0时，电容两端的电压为9V，顶部为正，t>0时它的自然响应是什么？可以看出单端口电路呈现的阻抗是：

显然，z1=–1/(R1C)=-1/(10ms)，p1=-1/[(R1+R2)C]=-1/(30ms)。此外，a1=[20/(10+20)]9=6V且b1=9/10=0.9mA。所以：