
电感位移传感器被广泛应用于微小位移量检测中,但在一些工程中现有传感器的测量精度和灵敏度达不到测量要求。针对这一问题,对传感器前段信号处理电路进行改进,在传感器上下线圈并联电容形成LC电路,利用LC电路谐振效应改善电路的性能,以提高信号源头的灵敏度;采用MulTIsim软件对半桥和全桥电路在并联不同大小的电容后的性能进行仿真,并用Matlab对生成的曲线进行最小二乘拟合,比较得出使电路性能最优的电容值和并联方法。结果表明在损失微小线性度的情况下可将灵敏度提高一倍。
电感位移传感器的实质,是将敏感元件的变化量转化成电压幅值的变化量来进行测量,其广泛应用于检测微小位移量的检测系统中,因此对电感传感器的测量精度和灵敏度要求很高。电感位移传感器的灵敏度是指输出电压的增量与侧头位移增量的比。在其他条件相同的情况下提高灵敏度可以提高系统的最小分辨率和精度。提高电感传感器灵敏度的方式有多种,但目前主要都是通过对电感传感器的信号调理电路的改进来实现。文中尝试通过谐振电路改变传感器的输出信号,从信号源头增大传感器灵敏度。这种方法相当于对传感器本身进行改进,使得它还可以与其他改进技术如:传感器激励源、输出信号处理、计算机软件补偿等兼容以共同提高整个系统的性能。
1 改进后电路的模型建立
1.1 半桥式改进电路
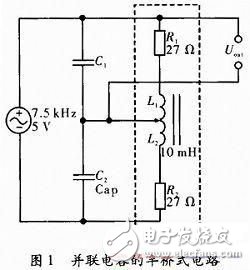
如图1如果没有C1和C2为普通半桥电路,虚线框中为电感传感器的等效电路,传感器测头的位移带动螺线管中铁芯上下移动,从而改变上下两个线圈的电感值。将两线圈等效成纯电阻和纯电感的串联,如图中R1和L1组成上线圈,R2和L2组成下线圈,输出接在上线圈上。实际传感器中线圈与输出的接线不会变,只是通过铁芯移动来改变电感,所以R1和R2固定不变。输出电压
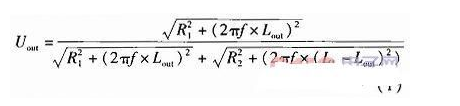
图1在上下两个线圈并联电容C1和C2后,分别形成了谐振回路I和回路II。如果铁芯在最下方时:回路II谐振,回路I失谐。当铁芯在最上方时:回路I谐振,回路II失谐。由于谐振电路在谐振时的阻抗会远大于失谐时的阻抗。可以定性地得出,铁芯在最下方时Uout的幅值会比没有电容小,在最上方时会比没有电容时大,所以灵敏度会增大。但在最下方和最上方中间的变化情况,以及它的线性度则需要后边仿真来确定。输出电压
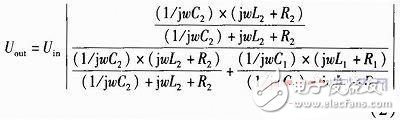
1.2 全桥式改进电路
普通全桥电路图2(a),传感器上下两线圈分别与匹配电阻R3和R4相连,在L1=L2时电桥平衡,当向上发生△X的位移时,铁芯上移,L1增大△L,L2减小△L,Uout的变化会比半桥方式增加近两倍,输出电压
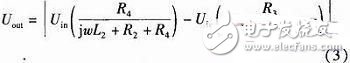
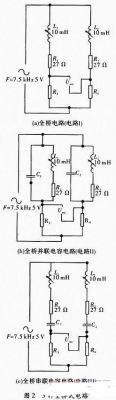
如图2(b)和图2(c)对上下两线圈分别采用并联和串联电容C1和C2的方式,形成谐振回路I和回路II,通过后续仿真观察这两种方式电路性能的变化情况。输出电压

2 电路的仿真
2.1 仿真平台及仿真条件
仿真平台使用MulTIsim,它是美国国家仪器(NI)有限公司推出的以Windows为基础的仿真工具,适用于板级的模拟/数字电路板的设计工作。它包含了电路原理图的图形输入、电路硬件描述语言输入方式,具有庞大的元器件库和全面的仪器仪表库和丰富的仿真分析能力。采用它来对改进前后的电路进行仿真。
在仿真之前,先结合工程实际情况对仿真条件进行一些设定:
(1)激励电源:频率为7.5 kHz,峰峰值为5 V的交流电。
(2)传感器:总电感值为10mH差动电感传感器,线性范围为3~7mH,电感的自身的电阻值为54Ω。
如上文所述R1和R2固定不变,所以R1和R2为27Ω。而对应的纯电感L1和L2,会随着位移线行变化,满足L1+L2=10 mH(3《L1《7,3《L2《7)。
2.2 仿真过程及结果
对于半桥时电路II由于希望铁芯在最下方时回路II谐振,最上方时回路I谐振,因为L1和L2的变化范围为3~7 mH。L2为7 mH时回路II谐振,L1为7 mH时回路I谐振。按照仿真条件计算C1=C2=65 nF。简化仿真不妨取C1=C2,在65 nF附近从55~100 nF间隔5 nF进行仿真,观察电路性能,仿真结果如图3所示。
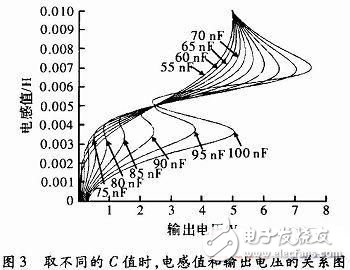
图中可以看出不同的电容值对电路的性能影响很大,如果选择不恰当,反而会使系统性能下降。只有选择适当容量的电容大小才能使测量灵敏度提高,同时保持尽量小的线性误差。所以选取曲线在L1=3~7 mH段时,灵敏度最高,线性度最好,进行最小二乘计算,它与普通半桥的对比如图4所示。
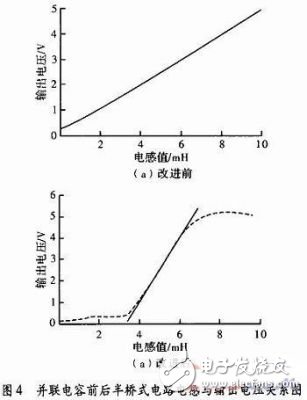
经Matlab计算普通半桥在3~7 mH段,电压变化范围1.5~3.5 V,电压对电感的灵敏度为0.5V/mH。线性度近似为1。对图4(b)采用最小二乘法拟合直线后,在3.8~6.3 mH段,输出电压的变化范围0.77~4.39 V。线性度可达2.39%,灵敏度为1.448 V/mH。
对全桥电路的仿真与半桥的方法类似,需要注意的是希望电桥在L1=L2=5 mL时平衡,所以对于匹配电阻的选取需要根据仿真条件计算
对于电路I:R3=R4=|jw×0.005+R1|=237 Ω;电路II:R3=R4=|(jwL+R1)∥(1/jwC1)|=817Ω;电路III:R3=R4=|jwL+R1+(1/jwC1)|=98Ω。
对于使用电容的电路,同样对不同的电容值条件下的电路进行仿真,选出性能最好的如图5所示。
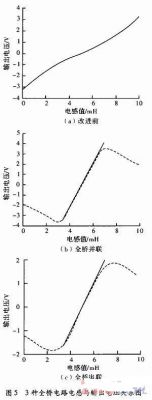
普通全桥在3.8~6.3 mH段,电压变化范围为-1.2~+1.3 V,电压对电感的灵敏度为1 V/mH。线性度近似为1.38。对图5(b)和图5(c)使用Matlab进行最小拟合直线如图所示,在3.8~6.3 mH段,并联方式输出电压的变化范围为-2.66~+2.66V,灵敏度为2.130V/mH线性度可达1.68%。串联方式的输出电压范围约为-1.25~+1.25V,灵敏度约为2.130V/mH线性度可达1.33%。
3 分析与结论
如表1所示,为各电路的灵敏度和线性度,可以在损失较小线性度条件下,将灵敏度提高。对于半桥虽然将灵敏度提高了近200%,但牺牲的线性度较大。串联电容的方式灵敏度几乎没有增大。性能最好的是并联电容后的全桥电路,灵敏度提升了113%,且损失的线性度较小,只比原来增大21.7%,而且实际应用中,可以通过软件补偿和事先标定来弥补线性度的不足。
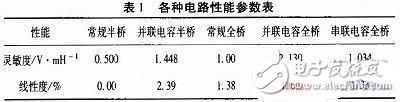
综合理论分析和仿真结果,在激励源确定和电感传感器参数确定的情况下,通过计算可以得到一个恰当的电容值,当在传感器的两部分线圈上并联这个电容时,测量的灵敏度会有显著提高,同时仍可以保持较好的线性度,从而达到改善和提高电感传感器性能和最小分辨率的目的。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)