
本蚊介绍了仿真的环境以及二阶锁相环的仿真过程,并对其仿真结果进行了分析。在前三章的理论基础上,通过使用MATLAB7.0进行了仿真。
验结果表明:用MATLAB进行的二阶锁相环仿真达到了最初的设想,锁相环的失锁、跟踪、捕获、锁定各个阶段均有体现。达到了最初仿真的要求。
(典型仿真案例)图
仿真使用的软件是MATLAB7.0。由于MATLAB仿真软件适合多学科、多种工作平台且功能强大、界面友好、方便快捷、语言自然并且开放性强的大型优秀应用软件,已经也已成为国内外高等院校高等数学、数值分析、数字信号处理、自动控制理论以及工程应用等课程的基本教学工具。使用Matlab对锁相环仿真的实现是方便快捷的。
仿真采用二阶锁相环仿真所采用的是二阶锁相环。这是由于我们实际应用中的绝大多数PLL,或者是二阶的,或者是通过忽略高阶效应(至少在初步设计时)而被设计成近似的二阶环路。鉴于二阶锁相环在实际应用的意义,所以在仿真采用了二阶锁相环。
MATLAB仿真程序代码% File: c6_nltvde.m
w2b=0; w2c=0; % iniTIalize integrators
yd=0; y=0; % iniTIalize differenTIal equaTIon
tfinal = 50; % simulation time
fs = 100; % sampling frequency
delt = 1/fs; % sampling period
npts = 1+fs*tfinal; % number of samples simulated
ydv = zeros(1,npts); % vector of dy/dt samples
yv = zeros(1,npts); % vector of y(t) samples
%
% beginning of simulation loop for i=1:npts t = (i-1)*delt;
% time
if t《20
ydd = 4*exp(-t/2)-3*yd*abs(y)-9*y; % de for t《20
else
ydd = 4*exp(-t/2)-3*yd-9*y;
% de for t》=20 end
w1b=ydd+w2b; % first integrator - step 1 w2b=ydd+w1b;
% first integrator - step 2
yd=w1b/(2*fs); % first integrator output w1c=yd+w2c; % second integrator - step 1 w2c=yd+w1c;
% second integrator - step 2
y=w1c/(2*fs); % second integrator output ydv(1,i) = yd; % build dy/dt vector yv(1,i) = y; % build y(t) vector end
% end of simulation loop
plot(yv,ydv) % plot phase plane xlabel(‘y(t)’) % label x axis ylabel(‘dy/dt’)
% label y zxis
% End of script file. % File: pllpost.m
%
kk = 0; while kk == 0 k = menu(‘Phase Lock Loop Postprocessor’,。。。
‘Input Frequency and VCO Frequency’,。。。
‘Input Phase and VCO Phase’,。。。
‘Frequency Error’,‘Phase Error’,‘Phase Plane Plot’,。。。
‘Phase Plane and Time Domain Plots’,‘Exit Program’);
if k == 1
plot(t,fin,‘k’,t,fvco,‘k’)
title(‘Input Frequency and VCO Freqeuncy’)
xlabel(‘Time - Seconds’);ylabel(‘Frequency - Hertz’);pause
elseif k ==2
pvco=phin-phierror;plot(t,phin,t,pvco)
title(‘Input Phase and VCO Phase’)
xlabel(‘Time - Seconds’);ylabel(‘Phase - Radians’);pause
elseif k == 3 plot
(t,freqerror);title(‘Frequency Error’)
xlabel(‘Time - Seconds’);ylabel(‘Frequency Error - Hertz’);pause
elseif k == 4
plot(t,phierror);title(‘Phase Error’)
xlabel(‘Time - Seconds’);ylabel(‘Phase Error - Radians’);pause
elseif k == 5
ppplot
elseif k == 6
subplot(211);phierrn = phierror/pi;
plot(phierrn,freqerror,‘k’);grid;
title(‘Phase Plane Plot’);xlabel(‘Phase Error /Pi’);
ylabel(‘Frequency Error - Hertz’);subplot(212)
plot(t,fin,‘k’,t,fvco,‘k’);grid
title(‘Input Frequency and VCO Freqeuncy’)
xlabel(‘Time - Seconds’);ylabel(‘Frequency - Hertz’);subplot(111)
elseif k == 7
kk = 1;
end
end % End of script file.
% File: pllpre.m
%
clear all % be safe
disp(‘ ’) % insert blank line
fdel = input(‘Enter the size of the frequency step in Hertz 》 ’);
fn = input(‘Enter the loop natural frequency in Hertz 》 ’);
lambda = input(‘Enter lambda, the relative pole offset 》 ’);
disp(‘ ’)
disp(‘Accept default values:’)
disp(‘ zeta = 1/sqrt(2) = 0.707,’)
disp(‘ fs = 200*fn, and’)
disp(‘ tstop = 1’) dtype = input(‘Enter y for yes or n for no 》 ’,‘s’);
if dtype == ‘y’
zeta = 1/sqrt(2);
fs = 200*fn;
tstop = 1;
else
zeta = input(‘Enter zeta, the loop damping factor 》 ’);
fs = input(‘Enter the sampling frequency in Hertz 》 ’);
tstop = input(‘Enter tstop, the simulation runtime 》 ’);
end %
npts = fs*tstop+1; % number of simulation points
t = (0:(npts-1))/fs; % default time vector
nsettle = fix(npts/10); % set nsettle time as 0.1*npts
tsettle = nsettle/fs; % set tsettle
% The next two lines establish the loop input frequency and phase
% deviations.
fin = [zeros(1,nsettle),fdel*ones(1,npts-nsettle)];
phin = [zeros(1,nsettle),2*pi*fdel*t(1:(npts-nsettle))];
disp(‘ ’) % insertblank line
% end of script file pllpre.m
% File: pll2sin.m
w2b=0; w2c=0; s5=0; phivco=0; %initialize
twopi=2*pi; % define 2*pi
twofs=2*fs; % define 2*fs
G=2*pi*fn*(zeta+sqrt(zeta*zeta-lambda)); % set loop gain
a=2*pi*fn/(zeta+sqrt(zeta*zeta-lambda)); % set filter parameter
a1=a*(1-lambda); a2 = a*lambda; % define constants
phierror = zeros(1,npts); % initialize vector
fvco=zeros(1,npts); % initialize vector
% beginning of simulation loop
for i=1:npts
s1=phin(i) - phivco; % phase error
s2=sin(s1); % sinusoidal phase detector
s3=G*s2;
s4=a1*s3;
s4a=s4-a2*s5; % loop filter integrator input
w1b=s4a+w2b; % filter integrator (step 1)
w2b=s4a+w1b; % filter integrator (step 2)
s5=w1b/twofs; % generate fiter output
s6=s3+s5; % VCO integrator input
w1c=s6+w2c; % VCO integrator (step 1)
w2c=s6+w1c; % VCO integrator (step 2)
phivco=w1c/twofs; % generate VCO output
phierror(i)=s1; % build phase error vector
fvco(i)=s6/twopi; % build VCO input vector
end
% end of simulation loop
freqerror=fin-fvco; % build frequency error vector
% End of script file.
function [] = pplane(x,y,nsettle)
% Plots the phase plane with phase in the range (-pi,pi)
ln = length(x);
maxfreq = max(y);
minfreq = min(y);
close % Old figure discarded
axis([-1 1 1.1*minfreq 1.1*maxfreq]); % Establish scale
hold on % Collect info for new fig
j = nsettle; while j 《 ln
i = 1;
while x(j) 《 pi & j 《 ln
a(i) = x(j)/pi;
b(i) = y(j);
j = j+1;
i = i+1;
end
plot(a,b,‘k’)
a = [];
b = [];
x = x - 2*pi;
end hold off title(‘Phase-Plane Plot’)
xlabel(‘Phase Error / Pi’)
ylabel(‘Frequency Error in Hertz’)
grid % End of script file.
% File: ppplot.m
% ppplot.m is the script file for plotting phase plane plots. If the
% phase plane is constrained to (-pi,pi) ppplot.m calls pplane.m.
kz = 0;
仿真过程及结果
上图是利用MATLAB提供的函数将计算结果图形化功能建立的。在运行程序后,就会出现上面的对话框,点击点击其中的任何一项就会出现相应的仿真图形。上图中包含了输入频率和VCO频率,输入相位和VCO相位,频率误差,相位误差,相位空间波特图,相位空间和时域,退出程序等选项。运行程序后出现如下指令:
Accept the tentative values: the first loop frequency is 5 第一循环频率
Enter y for yes or n for no 》 y
Enter the loop gain 》40 输入环路增益为
40 Enter the sampling frequency in Hertz 》 1200 输入采样频率
Enter tstop, the simulation runtime 》 5 仿真时间为5秒
设置好参数后运行程序,由上我们可知环路增益为40,仿真时间为5s,采样频率为1200Hz。接着点击上图锁相环处理框中的菜单,就能得到如下仿真图像。其中我们主要观察输入相位和VCO相位。
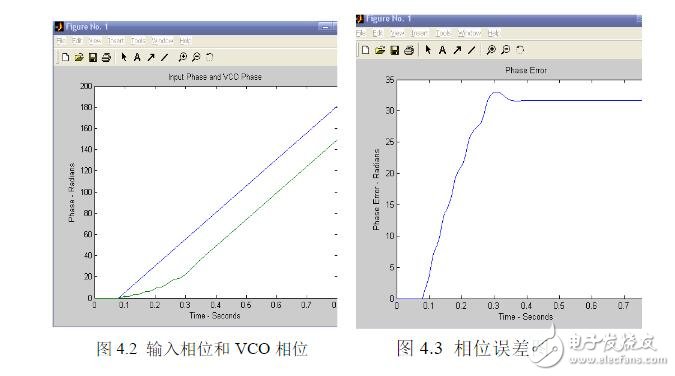
图4.2中蓝线为输入相位,绿线代表VCO相位,从图中可以看见随着时间的变化输入信号相位为线性,而VCO相位则是经历了一段曲线后斜率与输入信号相位斜率相同,输出相位跟随输入相位,达到稳定。图4.3中VCO的相位也是先经历了一段时间的曲线后变为一条直线达到稳定。根据锁相环的基本原理我们可知锁相环是个反馈网络,它是由输出信号(VCO产生)与参考频率在频率和相位上保持同步或者保持常数。由此我们可以看出锁相环工作后,在最初的一段时间中锁相环开始工作,输入信号经过鉴相器,环路虑波器后,将输出相位反馈给VCO压控振荡器,使压控振荡器与输入频率逐步实现同步,保持一个常数,实现锁定。其中经历了锁相环的失锁、跟踪、捕获、锁定,从而达到最后达到稳定状态。从开始到达到稳定的这段时间则为做捕获时间。
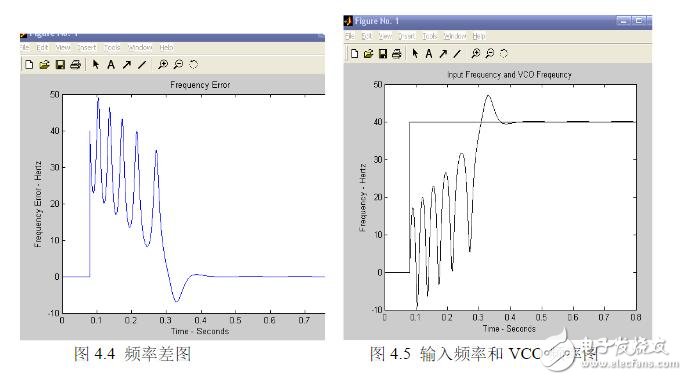
图4..4与图4.5也显示了锁相环工作后从失锁、跟踪、捕获、锁定的过程,过程。从不停的摆动到最后的直线状态,这个过程称为锁定过程。其中我们可以发现在捕捉过程中随着捕捉次数的增加,捕捉过程也变得较慢,这说明此时的的锁相环工作平率处在稳定工作的动态界限内,工作正常。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)