
线性相位滤波器是移动相位与频率成比例的滤波器,因此不改变波形而引入一常数延迟。线性相位滤波器是一个混合相位的滤波器,它按照与频率成正比地对频率分量作时移。因而在通常频带内相位移与频率的关系图是线性的,截距一定是2π倍,结果每个分量相等地延迟。也叫做延迟滤波器。这样的滤波器不产生相位畸变。如果截距是π的奇数倍,它会把子波反相。
第二类线性相位滤波器问题7.25* MATLAB分别设计第一类和第二类线性相位FIRDF
用窗函数法设计一个线性相位低通FIRDF,要求通带截止频率为0.3π, 阻带截止频率为0.5π,阻带最小衰减为40dB。选择合适的窗函数及其长度, 求出并显示所设计的单位脉冲响应h(n)的数据,并画出损耗函数曲线和相频 特性曲线,请检验设计结果。试不用fir1函数,直接按照窗函数设计法编程设计。做完后把题目修改为设计高通滤波器,为第二类线性相位,画出h(n) 1.第一类线性相位
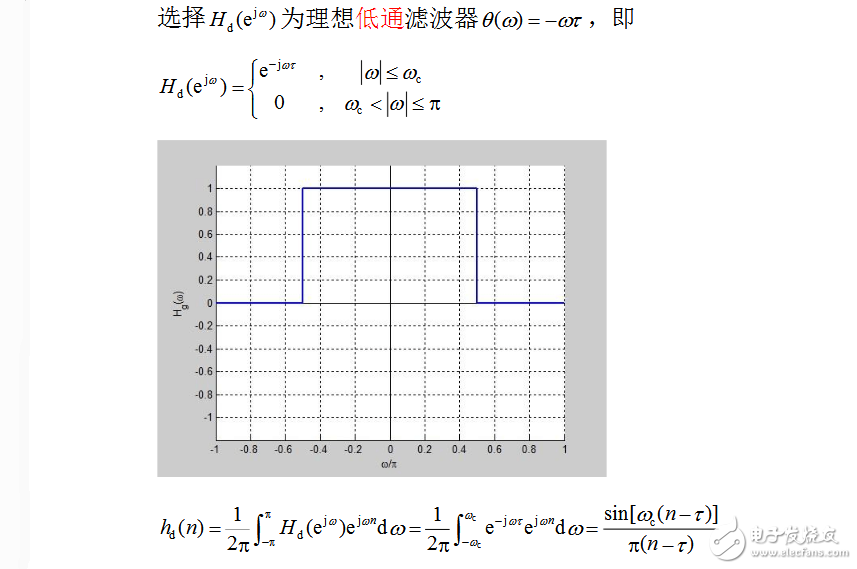
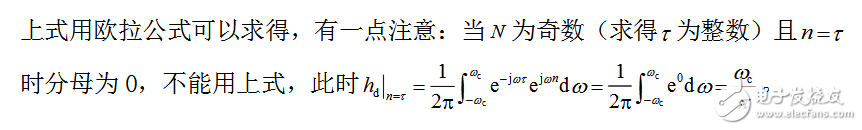
MATLAB Code:
clear all; close all; clc;
%--------------------- 第一类线性相位低通 ---------------------------
wp=0.3*pi;ws=0.5*pi; DB=ws-wp;
N=ceil(6.2*pi/DB); % 阻带最小衰减为40dB,所以选择汉宁窗
% 第二类线性相位低通h(n)长度N可为奇数或偶数 tau=(N-1)/2; wc=(wp+ws)/2; n=0:N-1;
hd=sin(wc*(n-tau))。/(pi*(n-tau));
if tau==ceil(tau) % 判断τ如果是整数
hd(tau+1)=wc/pi; % n=τ时分母为0,要替换这一项值 end
w=0.5*(1-cos(2*pi*n/(N-1))); h=hd.*w;
%------画图------ M=1024; Hk=fft(h,M); subplot(2,2,[1 2]); stem(n,h,‘。’);grid on; axis([0,30,-0.6,0.6]); xlabel(‘n’);ylabel(‘h(n)’); subplot(2,2,3); k=1:M/2;
w=2*pi*(0:M/2-1)/M;
plot(w/pi,20*log10(abs(Hk(k))));grid on;
xlabel(‘\omega/\pi’);ylabel(‘20lg|H_g(\omega)|’); subplot(2,2,4);
plot(w/pi,unwrap(angle(Hk(k))));grid on; xlabel(‘\omega/\pi’);ylabel(‘Ïàλ’)
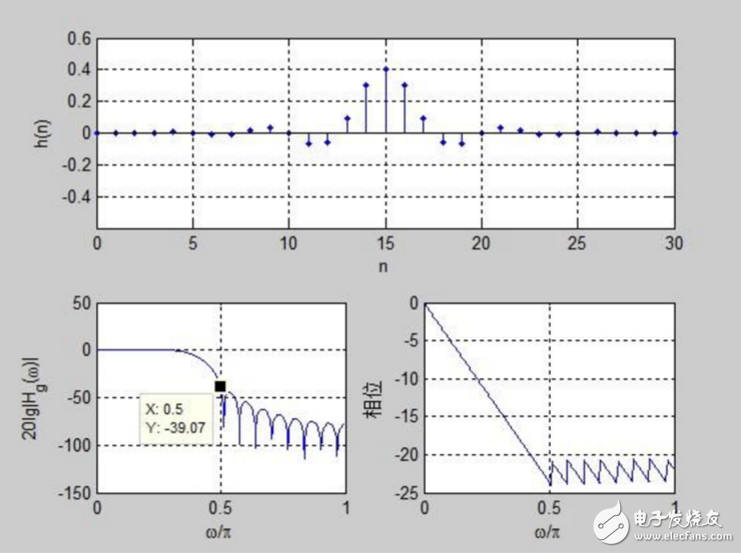
从图上看到截止频率为0.5π衰减为39.07dB,距离40dB指标还差点,可以增加h(n)长度N来提高衰减。
第二类线性相位
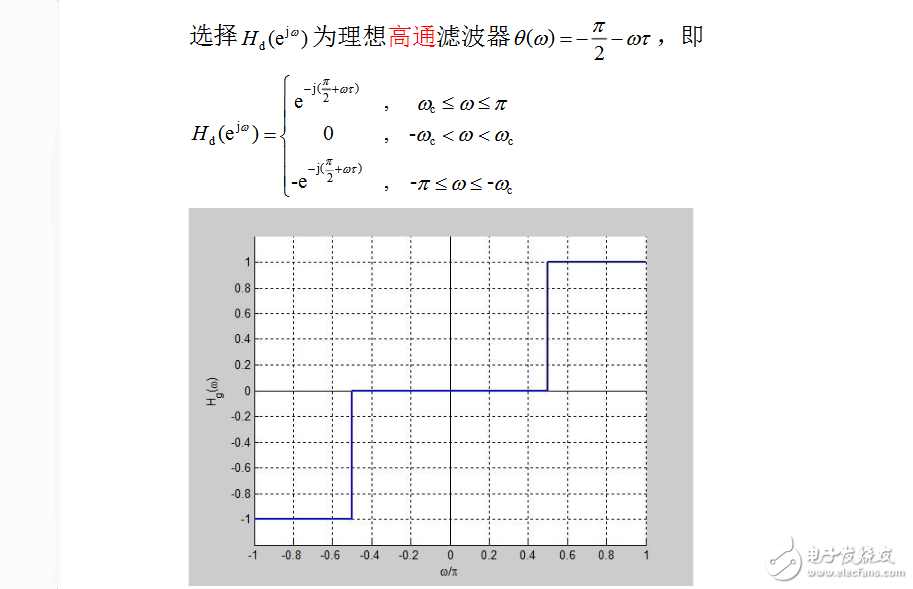
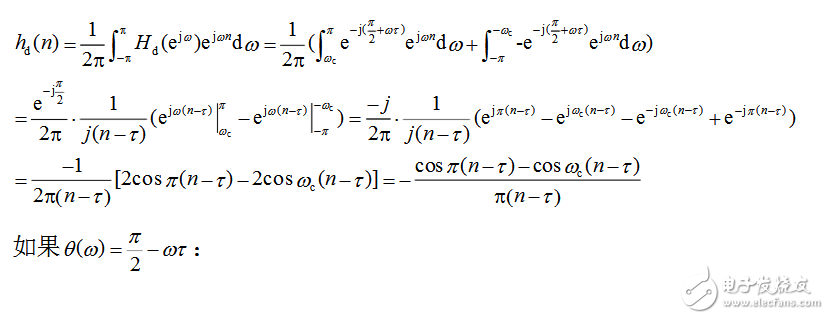

MATLAB Code:
%--------------------第二类线性相位高通 ----------------------- wp=0.5*pi;ws=0.3*pi; DB=wp-ws;
N0=ceil(6.2*pi/DB); % 阻带最小衰减为40dB,所以选择汉宁窗 N=N0+mod(N0,2); % 第二类线性相位高通N为偶数 tau=(N-1)/2; wc=(wp+ws)/2; n=0:N-1;
hd=-(cos(pi*(n-tau))-cos(wc*(n-tau)))。/(pi*(n-tau));% θ=-π/2+ωτ % hd=(cos(pi*(n-tau))-cos(wc*(n-tau)))。/(pi*(n-tau));% θ=π/2+ωτ w=0.5*(1-cos(2*pi*n/(N-1))); h=hd.*w;
%------画图------ M=1024; Hk=fft(h,M); figure;
subplot(2,2,[1 2]); stem(n,h,‘。’);grid on; axis([0 30 -0.6 0.6]); xlabel(‘n’);ylabel(‘h(n)’); subplot(2,2,3); k=1:M/2;
w=2*pi*(0:M/2-1)/M;
plot(w/pi,20*log10(abs(Hk(k))));grid on;
xlabel(‘\omega/\pi’);ylabel(‘20lg|H_g(\omega)|’); subplot(2,2,4);
plot(w/pi,unwrap(angle(Hk(k))));grid on; xlabel(‘\omega/\pi’);ylabel(‘Ïàλ’)
采用hd=-(cos(pi*(n-tau))-cos(wc*(n-tau)))。/(pi*(n-tau));% θ=-π/2+ωτ :得到下图
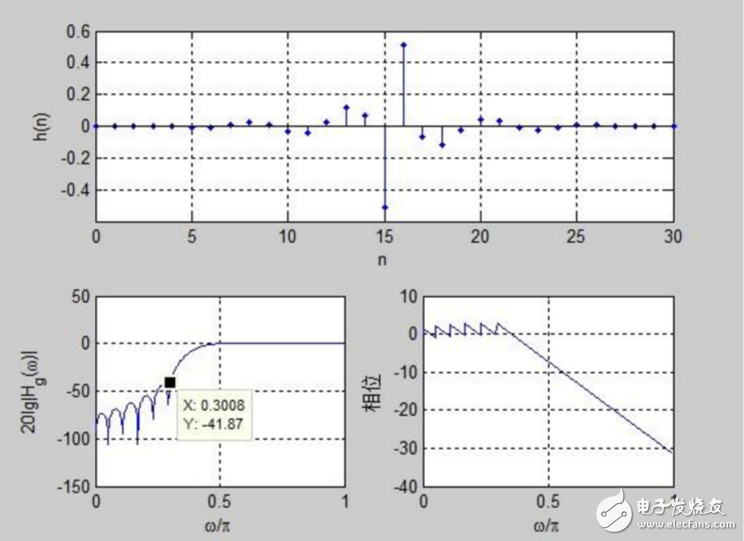
采用hd=(cos(pi*(n-tau))-cos(wc*(n-tau)))。/(pi*(n-tau));% θ=π/2+ωτ :得到下图
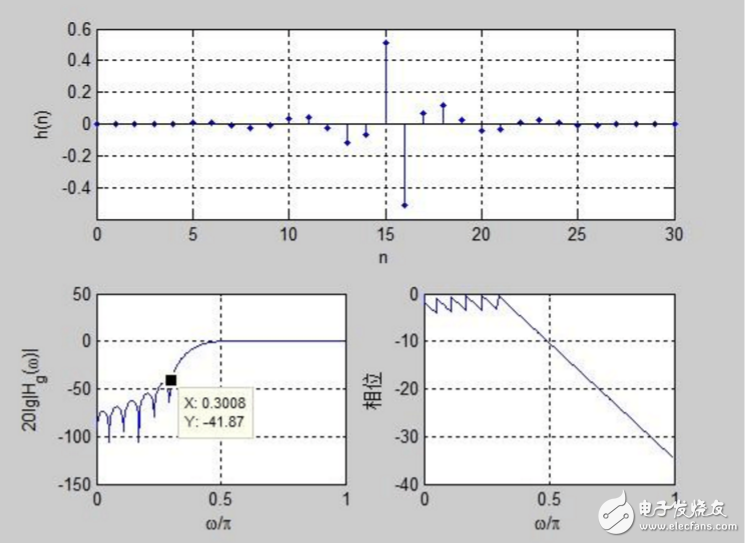
可以看出相移不同,h(n)图像不同!
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)