优化的BP神经网络在电子设备故障诊断中的应用

优化的BP神经网络在电子设备故障诊断中的应用

近些年来，由于计算机技术、信号处理、人工智能、模式识别技术的发展，促进了故障诊断技术的不断发展，大型复杂电子设备的出现，使得人们更迫切地希望能提高整体可靠性与维修性，这就给故障诊断提出了更高的要求。因此，对故障诊断技术的研究有着重要的理论及现实意义。

1 BP神经网络故障诊断模型

一个神经网络用于故障诊断时，主要包括三层：输入层，即从设备对象接收各种故障信息和现象；中间层，是把从输入层得到的故障信息，经内部的学习和处理，转化为针对性的解决办法；输出层，是针对输入的故障形式，经过调整权值后得到的故障处理方法。对于一个新的输入状态信息，训练好的网络将由输出层给出故障识别结果。BP神经网络故障诊断模型如图1所示。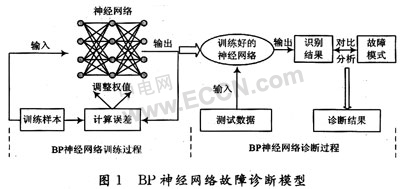


2 BP神经网络的优化——共轭梯度法   

虽然神经网络模型已成功应用于模式识别、函数逼近、时间序列预测等领域，但是由于BP学习算法仅改变网络的连接值和阈值，不改变网络的拓扑结构，因此BP网络在处理具体问题时还存在收敛速度慢，易陷入局部极小值等缺点。为了解决BP网络训练的缺点，人们提出了多种有益的改进方法。

本文研究了共轭梯度法对BP神经网络进行优化设计，基本思想如下：

传统的前向多层网络的BP学习算法实质上是无约束的最速下降法，改进的BP算法是对最速下降法作了一些约束；而共轭梯度法则是介于最速下降法和牛顿法之间的一种方法，它仅需要利用一阶导数信息，不仅克服了BP学习算法收敛慢的缺点，又避免了存储和计算牛顿法所需要的二阶导数信息。共轭梯度法的计算步骤和最速下降梯度法差别不大，主要差别在于搜索方向不同，即每一步的方向不是梯度的负方向，而是一种共轭的方向。由原来的负梯度方向加上一个修正项得到共轭方向，也就是使得最速下降法具有共轭性，从而提高算法的有效性和可靠性。共轭梯度法应用于神经网络中的目的是求误差函数E(W)的最小值。算法主要是利用共扼梯度方向来修正权值W，使W的确定更为快速，计算过程如下；   

(1)初始化权值W1，令k=1；
   
(2)计算网络的负梯度矢量：
   
设p1=r1=-E’(W1)，式中E’(W1)是根据BP算法求出的负梯度。

(3)计算步长ak：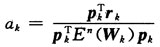

式中：En(W1)为误差函数对权值矢量W的二次导数。

(4)调整权值：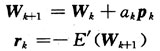

(5)如果k除以样本数N的余数为零时，pk+1=rk+1，否则计算新的搜索方向：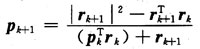

(6)如果梯度方向∣rk∣>ε，则置k=k+1，否则停止，Wk+1为所求权值矢量。

3诊断实例

现以一电子设备为诊断对象，验证优化的BP神经网络算法。样本数据从测试口测试获得，一共6个测试点，10个板卡故障。诊断步骤如下：

(1)故障特征提取

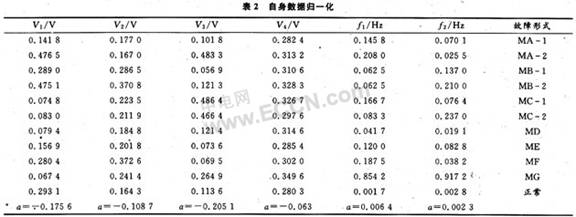
表1为实验测得的故障样本数据；表2为归一化后的数据，其激活函数采用S型函数f=1／(1+e-ax)；表3为神经网络的目标输出模式，1表示有故障，0表示正常。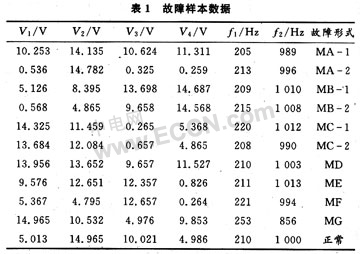




(2)BP网络的训练

取输入节点N1=6，输出节点N3=11，隐层节点采用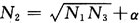，a取1～10，本实验中a取7(根据训练误差曲线调整而得)，N2=15。学习率η=0.2，训练误差E<0.005，最大训练次数n=1 000。图2为BP网络的训练误差曲线。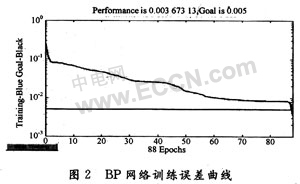


(3)BP网识别结果分析

①用样本自身数据输入训练好的神经网络中，其识别结果见表4。与故障模式对比分析可知，自身数据检测正确率为100％。可见，该网络达到了训练的要求。

②任取4组测试数据见表5，观察其识别结果。表6为归一化后的测试数据，表7为识别结果。与故障模式对比可知，第一组数据对应的故障是MA-1；第二组数据对应的故障是MB-2；第三组数据对应的故障是MD；第四组数据对应的故障是MG。由此可见，本网络不仅能识别样本本身的故障，而且能准确诊断样本以外的数据故障。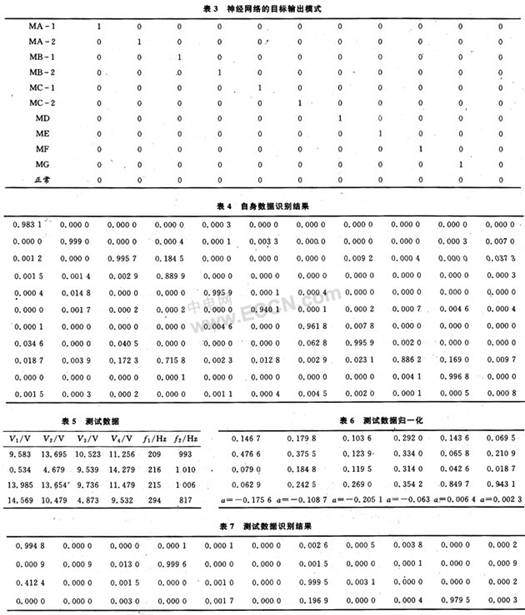



4 结  语

本次实验中的BP神经网络采用共轭梯度法进行优化设计，由实验数据可知，该网络能够准确诊断数据的故障状态，可见，该方法能够成功应用于设备的故障诊断中。故障诊断是一门实用性很强的技术，因此只有在实际应用中才能体现它的价值，目前在理论研究方面虽有不少进展，但真正在工程实践中成功应用的实例还较少，因此如何将先进的故障诊断理论与方法应用到实际中，还有待更深入的研究。