
三角函数的计算是个复杂的主题,有计算机之前,人们通常通过查找三角函数表来计算任意角度的三角函数的值。这种表格在人们刚刚产生三角函数的概念的时候就已经有了,它们通常是通过从已知值(比如sin(π/2)=1)开始并重复应用半角和和差公式而生成。
现在有了计算机,三角函数表便推出了历史的舞台。但是像我这样的喜欢刨根问底的人,不禁要问计算机又是如何计算三角函数值的呢。最容易想到的办法就是利用级数展开,比如泰勒级数来逼近三角函数,只要项数取得足够多就能以任意的精度来逼近函数值。除了泰勒级数逼近之外,还有其他许多的逼近方法,比如切比雪夫逼近、最佳一致逼近和Padé逼近等。
所有这些逼近方法本质上都是用多项式函数来近似我们要计算的三角函数,计算过程中必然要涉及到大量的浮点运算。在缺乏硬件乘法器的简单设备上(比如没有浮点运算单元的单片机),用这些方法来计算三角函数会非常的费时。为了解决这个问题,J. Volder于1959年提出了一种快速算法,称之为CORDIC(COordinate RotaTIon DIgital Computer) 算法,这个算法只利用移位和加减运算,就能计算常用三角函数值,如Sin,Cos,Sinh,Cosh等函数。 J. Walther在1974年在这种算法的基础上进一步改进,使其可以计算出多种超越函数,更大的扩展了Cordic 算法的应用。因为Cordic 算法只用了移位和加法,很容易用纯硬件来实现,因此我们常能在FPGA运算平台上见到它的身影。不过,大多数的软件程序员们都没有听说过这种算法,也更不会主动的去用这种算法。其实,在嵌入式软件开发,尤其是在没有浮点运算指令的嵌入式平台(比如定点型DSP)上做开发时,还是会遇上可以用到Cordic 算法的情况的,所以掌握基本的Cordic算法还是有用的。
从二分查找法说起
先从一个例子说起,知道平面上一点在直角坐标系下的坐标(X,Y)=(100,200),如何求的在极坐标系下的坐标(ρ,θ)。用计算器计算一下可知答案是(223.61,63.435)。
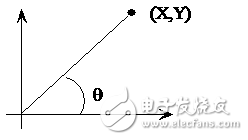
图 1 直角坐标系到极坐标系的转换

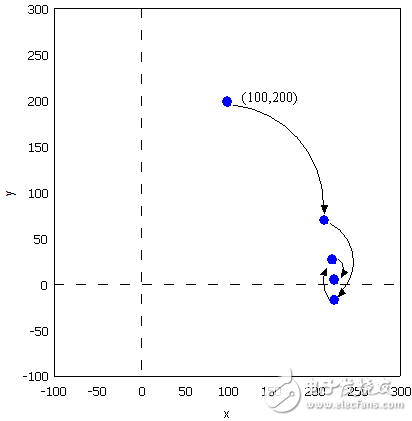
可能有读者会问,计算中用到了 sin 函数和 cos 函数,这些值又是怎么计算呢。很简单,我们只用到很少的几个特殊点的sin 函数和 cos 函数的值,提前计算好存起来,用时查表。
下面给出上面方法的C 语言实现。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)