基于FPGA的Cordic算法实现的设计与验证_技术

CORDIC（Coordinate RotaTIon Digital Computer）算法即坐标旋转数字计算方法，是J.D.Volder1于1959年首次提出，主要用于三角函数、双曲线、指数、对数的计算。该算法通过基本的加和移位运算代替乘法运算，使得矢量的旋转和定向的计算不再需要三角函数、乘法、开方、反三角、指数等函数。

本文是基于FPGA实现Cordic算法的设计与验证，使用Verilog HDL设计，初步可实现正弦、余弦、反正切函数的实现。将复杂的运算转化成FPGA擅长的加减法和乘法，而乘法运算可以用移位运算代替。Cordic算法有两种模式，旋转模式和向量模式。可以在圆坐标系、线性坐标系、双曲线坐标系使用。本文线初步实现在圆坐标系下的两种模式的算法实现。

Cordic算法简化

旋转模式，迭代位移算法。假设有一点P0（x0，y0），经过逆时针旋转角度θ，到达点Pm（xm，ym），我们根据数学运算可以得到公式如下：

xm = x0cosθ - y0sinθ = cosθ（x0 – y0tanθ）

ym = y0cosθ + x0sinθ = cosθ（y0 – x0tanθ）

如果不考虑旋转后的向量模值，只考虑旋转角度，即去掉cosθ，得到如下方程式。这里旋转的角度的正确的，但x和y的值增加。cosθ值是小于等于1的，值大于等于1，所以模值应该增大。我们不能通过适当的数学计算去掉cosθ，但是去掉cosθ项可以方便我们后面的坐标平面旋转的计算。这里称为伪旋转。

xm = x0 – y0tanθ

ym = y0 – x0tanθ

Cordic的方法核心就是伪旋转，将旋转角θ细化成若干个大小固定的角度θi，规定θi满足tanθi = 2^-i，通过一系列的迭代旋转，每次旋转θi，i为迭代次数，规定∑θi的范围即旋转角度θ的范围为［-99.7， 99.7］。如果θ的大于这个范围则可通过三角运算 *** 作转化到该范围的角度。

我们通过事先将所有每次旋转的角度计算出来，由于每次旋转的角度是固定的，所以经过i次旋转的∑θi可能会超过θ，所以就必须设置一个方向值di，如果旋转角度之和已经小于θ，则di为1，下次旋转继续为顺时针旋转，如果旋转角度之和大于θ，则di为-1，下次旋转为逆时针。设置zi+1为旋转剩余角度，zi+1 = z0 – dizi，z0 = θ，随着i值得增大，zi+1会趋向于0时，即旋转结束。di与zi的符号位相同。

采用伪旋转的方法，每次提出一个cosθi，旋转结束后会产生一个∏cosθi的累乘，一旦我们确定了迭代次数，∏cosθi就是一个常数，迭代公式可写为。这是将cosθi提出、tanθi 替换成 2^-i后的结果。di与zi的符号位相同。

xi+1 = xi - di * yi * 2^-i

yi+1 = yi + di * xi * 2^-i

zi+1 = z0 - di * θi

设迭代i = n - 1，那么旋转n次后得到Pm的坐标应该为（xn * ∏cosθi， yn * ∏cosθi）。应为每次迭代都会提出一个cosθi，旋转n次后的xn和yn就会少乘一个∏cosθi，所以实际上最终的Pm坐标角度近似于（xn * ∏cosθi， yn * ∏cosθi）。

xn * ∏cosθi = x0cosθ - y0sinθ

yn * ∏cosθi = y0cosθ + x0sinθ

xn = 1/∏cosθi （x0cosθ – y0sinθ）

yn = 1/∏cosθi （y0cosθ – x0sinθ）

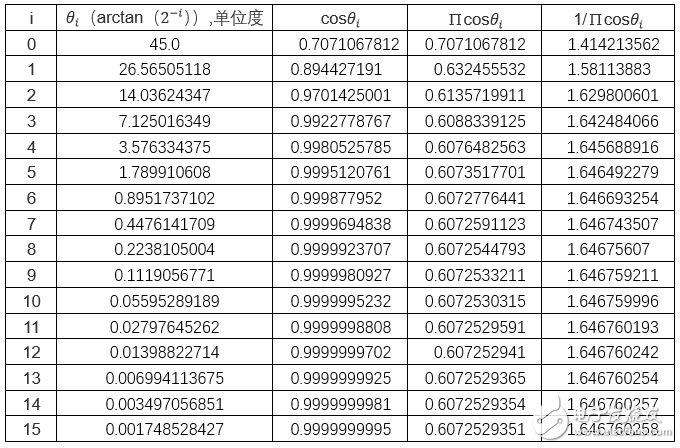
伸缩因子，KN = 1 / ∏cosθi，已知迭代次数，我们可以预先计算KN的值。如下这是博主使用MATLAB计算出的迭代结果数值。

xn =KN （x0cosθ – y0sinθ）

yn = KN （y0cosθ – x0sinθ）

从上表可以得出，我们预先计算出KN的值，然后令x0 = ∏cosθi，y0 = 0，则上述公式可化简为

xn = cosθ

yn = sinθ

即可实现正弦、余弦 *** 作了。

旋转模式

总结一下，Cordic算法旋转模式使用Verilog HDL的实现流程

（1）确定迭代次数，将每次迭代的角度计算出来，预先定义为参数，为了避免浮点运算，将角度值向左移位16位，取整数部分。

（2）根据迭代公式进行迭代计算，本设计取16次迭代，从上表可以看出，当迭代次数越大时，1/∏cosθi会趋向于一个确定值。如果对结果精度要求更高，可以设置更高的迭代次数，根据迭代次数，可以将伸缩因子KN = 1/∏cosθi计算出来。同样将其左移16位。

xi+1 = xi - di * yi * 2^-i

yi+1 = yi + di * xi * 2^-i

zi+1 = z0 - di * θi

（3）设置x0 = ∏cosθi，y0 = 0，则求出x16 = cosθ，y16 = sinθ。

这里需要注意的是，我们在进行迭代运算的时候，将2^-i变成移位运算，对于正余弦来说是有正负的，所以在一开始定义的时候，就应该定义成有符号数，Verilog中也可以定义有符号数，最高位表示符号位，定义如下

迭代寄存器定义为有符号数，那么我们移位运算就不能用》》逻辑右移《《逻辑左移或来移位了，而是用》》》算术右移和《《《算术左移。逻辑左移也就相当于算数左移，右边统一添0 ，逻辑右移，左边统一添0 ，算数右移，左边添加的数和符号有关。

例如1010_1010，［］是添加的位

逻辑左移一位：0101_010［0］

算数左移一位：0101_010［0］

逻辑右移一位：［0］101_0101

算数右移一位：［1］101_0101

迭代运算采用16级流水线，进行运算，最终需要判断输出的正余弦值在哪个象限，前面讲旋转角度θ的范围为［-99.7，99.7］，不在这个范围我们要进行三角运算使其满足这个范围，当输入的角度小于90度即可进行计算，当输入角度大于90度小于180度，将输入角度减去90度并设定当前角度处于第二象限，然后进行计算，当输入角度大于180度小于270度，将输入的角度减去180度设置当前角度处于第三象限，进行计算，当输入的角度大于270度，减去270设置当前角度处于第四象限，进行计算。象限的设定通过quarant寄存器实现。

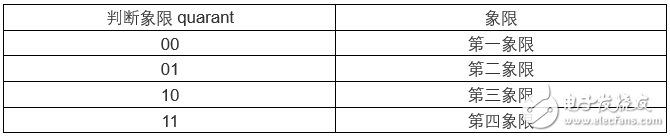
如果角度在第一象限，sin（x） = sin（a），cos（x） = sin（a）最后的结果x16 = cosθ， y16 = sinθ，这里我想起了那句口诀，一全正，二正弦，三正切，四余弦

如果角度在第二象限，sin（x） = sin（a+90） = cos（a），cos（x） = cos（a+90） = -sin（a）

如果角度在第三象限，sin（x） = sin（a+180） = -sin（a），cos（x） = cos（a+180） = -cos（a）

如果角度在第四象限，sin（x） = sin（a+270） = cos（a），cos（x） = cos（a+270） = -sin（a）

对于正数，我们直接赋值输出，负数，这里使用有符号数表示，将其取反加1即可。最终使用modelsim对算法进行仿真，从波形图上看已经初步实现了sin，cos函数。

向量模式

Cordic算法在向量模式下的计算方法和旋转模式基本上是类似的，设有一点P0（x0， y0），经过顺时针旋转角度到与轴重合，得到点Pm（xm， ym），即ym = 0。

xm = x0cosθ - y0sinθ = cosθ（x0 – y0tanθ）

ym = y0cosθ + x0sinθ = cosθ（y0 – x0tanθ） = 0

我们设置x0 = x， y0 = y， z0 = 0，迭代次数为16，经过16次迭代后得到zn = θ = arctan（y/x）和坐标所代表的向量的模值d = xm = xn * ∏cosθi，di与yi方向相反，即当时结束运算。实现方法为判断yi的符号位，符号位为1，di为1，符号位为0，di为-1。

xi+1 = xi - di * yi * 2^-i

yi+1 = yi + di * xi * 2^-i

zi+1 = z0 - di * θi

关于反正切函数，由于在［-99.7°，99.7°］范围内，所以我们输入向量P0（x0， y0）时，需要保证其在第一、四象限。

下面是使用MATLAB计算出来的数据和FPGA计算出来的数据进行比较。