小波去噪方法及步骤_小波去噪方法的比较

本文主要介绍小波分解与重构法、非线性小波变换阈值法、平移不变量小波法以及小波变换模极大值法这4种常用的小波去噪方法。将它们分别用于仿真算例的去噪处理，并对这几种方法的应用场合、去噪性能、计算速度和影响因素等方面进行比较。

选择了Matlab软件中的仿真信号Blocks作为原始信号，信号长度（即采样点数）N=2048，如图1a所示。由于该信号中含有若干不连续点和奇异点，因此用以下几种方法对图1b中叠加了高斯白噪声的Blocks信号（信噪比为7）进行去噪处理，能够很清楚地比较出这几种方法的去噪性能。

图1  原始信号和含噪信号的时域波形

一、小波去噪方法 1、小波分解与重构法去噪

小波分解与重构的快速算法，即Mallet算法。据这一算法，若fk为信号f（t）的离散采样数据，fk=c0，k，则信号f（t）的正交小波变换分解公式为：

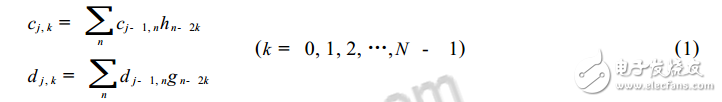
其中，cj，k为尺度系数;dj，k为小波系数;h、g为一对正交镜像滤波器组（QMF）;j为分解层数;N为离散采样点数。

小波重构过程是分解过程的逆运算，相应的重构公式为：

小波的多分辨分析特性能将信号在不同尺度下进行多分辨率的分解，并将交织在一起的各种不同频率组成的混合信号分解成不同频段的子信号，因而对信号具有按频带处理的能力。应用小波分解与重构的方法去噪具体步骤是：根据需要，将含有噪声信号在某一尺度下分解到不同的频带内，然后再将噪声所处的频带置零（或直接提取有用信号所在的频带），进行小波重构，从而达到去噪的目的。

图2是用小波分解与重构法进行去噪的结果。采用的小波是近似对称的Symmlet8小波，小波分解层数是4，其中图2a是将图1b中的含噪信号进行4层小波分解的结果。从中可以看出，信号的能量主要集中于低频的少数小波系数上，而噪声的能量则分散于整个小波变换域。图2b是提取图2a中的前256个小波系数进行重构，也就是提取尺度4上的低频系数和高频系数进行重构的结果。

图2  小波分解与重构法去噪

2、非线性小波变换阈值法去噪

非线性小波变换阈值法也称为“小波收缩”（waveletshrinkage），其去噪方法如下：

假设一个叠加了高斯白噪声的有限长信号可以表示为

其中，zi是一个标准的高斯白噪声，即z～N（0，1），R是噪声级。若要从被噪声污染的信号yi中恢复出原始信号xi，则Donoho的去噪方法分为以下3个步骤：

（1）计算含噪声信号的正交小波变换。选择合适的小波和小波分解层数j，将含噪信号运用（1）式进行小波分解至j层，得到相应的小波分解系数。

（2）对分解得到的小波系数进行阈值处理，其阈值的处理方法有2种：

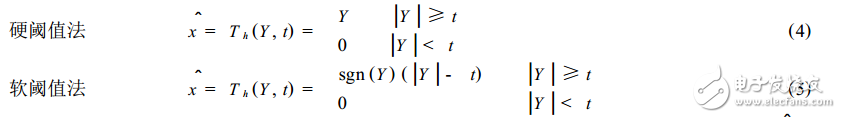
（3）进行小波逆变换。将经阈值处理过的小波系数用（2）式重构，得到恢复的原始信号估计值xd。

小波变换具有一种“集中”的能力，它能将信号的能量集中到少数小波系数上;而白噪声在任何正交

基上的变换仍然是白噪声，并且有着相同的幅度。相对来说，信号的小波系数值必然大于那些能量分散且幅值较小的噪声的小波系数值。选择一个合适的阈值，对小波系数进行阈值处理，就可以达到去除噪声而保留有用信号的目的。该方法能得到原始信号的近似最优估计，并且具有非常广泛的适应性。

图3和图4分别是采用Donoho的非线性小波变换阈值法以及平移不变量小波法去噪得到的结果。这2种方法均选用Haar小波，小波分解层数是5。二者均采用软阈值，阈值大小t=2log（N），其中N为信号长度。

图3  软阈值法去噪

图4  平移不变量小波法去噪