基于DSP48E硬核乘加单元的高效并行相关时差估计器设计与实现

从相关时差估计的基本原理出发，提出了一种并行时域相关结构，基于这种并行结构设计实现了一种简单高效的时差估计器。与传统频域相关时差估计器相比，这种时差估计器的主要优点是提高了运算效率，运算周期大为缩短，可以满足实时高精度时差估计的需求，同时结构简单，硬件资源开销小，易于设计实现。实际测试结果验证了上述结论。 无源时差定位系统利用多个观察站接收目标辐射源的信号，通过估计各个观察站接收信号之间的到达时间差，完成对目标辐射源的定位，具有作用距离远、隐蔽性强、定位精度高等优点。通常是通过对各个接收站的中频信号进行互相关，比较接收信号之间的相似性来得到高精度的到达时间差估计结果[1-2]。    对于无源时差定位中所处理的雷达信号，一般可以检测出脉冲的到达时间,也就大体知道了到达时间差[3]，从而可通过控制相关序列的采样时机，只求解相关函数相关峰附近的相关值就可获得时差信息。而相关函数的计算一般利用FFT/IFFT快速算法进行频域相关，频域相关会同时计算全部相关信息，在已知粗略时差范围时效率并不高（对于长度为N的采样序列，用频域相关法估计时差需要进行3个2N点FFT/IFFT运算和2N次复数乘法），而且大点数FFT/IFFT的工程实现也非常困难，运算时间与硬件资源开销严重，不适于进行实时时差估计[4- 5]。    本文利用时域相关可只求解部分相关值的优势，设计实现了一种并行相关结构的时差估计器，大大缩减了运算时间，可以满足实时时差估计的需求，同时简化了硬件结构、降低了硬件开销与实现难度。1 基本原理[6-8]    假设辐射源辐射的信号为实信号s(t)，被两个接收机接收的信号分别为x(t)和y(t)，具有不同的噪声和时间延迟，两信号可表示为：

    由于信号与噪声互不相关，Rsn1=Rsn2=0,因此可得到：

    若需±m(0

对乘累加器每个周期所进行的乘运算进行调整，如表2所示。从中可以发现：相关结果未发生变化；每个乘周期所有乘累加器的输入都相同；第i个乘累加器当前周期的x输入为第i-1个乘累加器上一乘周期的x输入。由此，可设计一种并行流水结构来避免多个乘累加器同时工作时对数据吞吐率的要求。

    如图1所示，每个乘累加器的y输入相同，x输入则由上一个乘累加器的x输入经过一延迟寄存器得到，整个并行相关器每个周期只需读入两个新的输入数据，数据吞吐率得以大大降低。需注意的是，为了求得±m(0

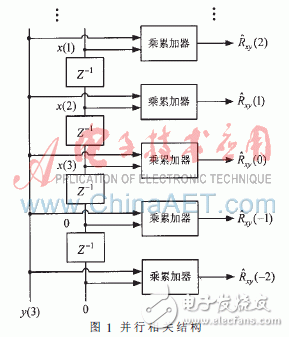
    在实际进行设计时，上述流水结构依然面临难题。在乘累加器较多、时钟速率与采样位数较高的情况下，需要添加复杂的时序约束，才能保证每个乘累加器的y输入都接收到正确数据，而这实现起来是非常困难的，有时是不可能的。为了解决这个问题，参照对x输入流水化的方法，对y输入也进行流水化处理，改进为图2所示的并行流水结构。此结构在数据输入完毕后，各个乘累加器将依次输出相关结果，且在第一个乘累加器输出结果后，做相应的清零，就可以进行新数据的相关运算。

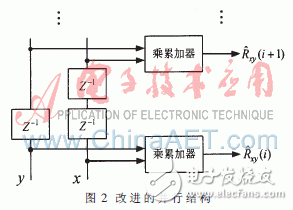
2.2 基于DSP48E的并行相关器    Xilinx公司的Virtex-5系列FPGA具有多个集成了补码乘法器和48位累加器的DSP48E硬核乘加单元[11]。每个硬核乘加单元不仅支持最高550 MHz的乘法累加器工作模式，并且带有用于增强性能的可选流水线级数。相邻的单元之间具有专用的级联通道，不需消耗片上逻辑与布线资源，只需进行简单的配置（图3）即可实现图2所示的并行相关结构。单个DSP48E硬核乘加单元有5个时钟的流水延迟，具有2m+1个乘加单元的并行相关结构,进行相关运算所需时间为:

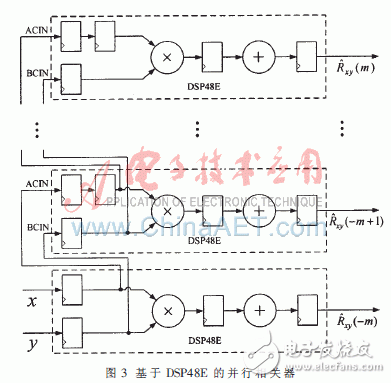
2.3 m的选取[12-13]    为了确定m的取值，需要知道两接收机信号的粗略到达时间差及误差。当采用线性检波和固定门限检测时，到达时间测量的均方根变化为：

3 实验及结果分析3.1 性能比较分析   利用式(8)可求得时差估计器N=4 096点的相关运算时间，将运算时间与硬件资源消耗列于表3。为便于比较，将FPGA实现N=8 192点FFT的运算时间与硬件资源消耗同时列出。

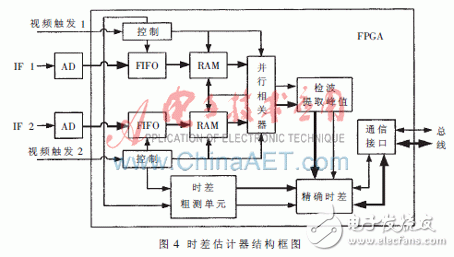
    频域互相关法测时差共需要进行3个8 192点FFT/IFFT和8 192次复数乘法，结合上表可知，频域互相关法的硬件资源消耗与运算周期都将远远高于本文设计的时差估计器。在fclk为250 MHz的情况下，本文设计的时差估计器可对重频最高为58 kHz的雷达信号进行实时时差估计，无需复杂的时序约束设计，避免了高系统时钟对系统稳定性的影响，降低了硬件实现难度。3.2 实验结果分析利用该时差估计器对常用雷达信号进行测试，各信号参数设置如下：　 Signal 1：单载频脉冲信号，脉宽0.5 μs；　 Signal 2：单载频脉冲信号，脉宽1 μs；    Signal 3：线性调频信号，脉宽100 μs，带宽10 Mb/s。    测试结果（如表4）表明该时差估计器可以完成无源定位中对雷达信号的高精度实时时差估计，估计精度优于10 ns。

    本文从时域互相关的原理出发，优化设计并实现了一种基于DSP48E硬核乘加单元的高效并行相关时差估计器，与频域互相关法测时差相比，以更少的硬件资源实现更快的运算速度，在降低硬件实现难度的同时提高了系统稳定性。实际测试结果表明,该时差估计器可以满足无源定位中高精度实时时差测量的要求，具有重要的应用价值。参考文献[1] 龚享铱, 杨广平. 基于相参脉冲时频估计的到达时间差精确估计算法研究[J].电子与信息学报，2007,29(5):1058-1060.[2] 孙仲康，周一宇，何黎星. 单多基地有源无源定位技术[M]. 北京：国防工业出版社, 1996.[3] 胡来招. 无源定位[M]. 北京: 国防工业出版社, 2004.[4] KENDALL W B. A new algorithm for compuTIng correlaTIons[J].IEEE TransacTIons on Computers.1974,23(1):88-90.[5] 蒋毅凯, 李国通, 杨根庆. 频域相关器在低轨小卫星中的应用[J].系统工程与电子技术,2004,26(9):1155-1158.[6] 孟嘉,黄高明,杨绿溪.欠采样带通信号时延估计算法[J].信号处理,2006,22(1):65-69.[7] 宋杰,唐小明,何友.脉冲制无源雷达动目标时延快速估计方法[J].电子科技大学学报,2009,38(6):908-912,978.[8] KNAPP C H, CARTER G C. The generalized correlaTIon method for estimation of time delay[J]. IEEE Transactions  on Acoustics, Speech, and Signal Processing,1976, 24(4):320-327.[9] SCARBROUGH K, AHMED N, CARTER G C. On the simulation of a class of time delay estimation algorithms[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981,29(3):534-540.[10] 戈立军, 吴虹, 金宇昂. 一种低复杂度数字互相关器的设计及其FPGA实现[J]. 南开大学学报(自然科学版).2009,42(4):43-47.[11] Xilinx, Inc. Xilinx Virtex-5 Family FPGAs[EB/OL].[12] SKOLNIK M I. Introduction to Radar Systems[M]. Seconded. New York: McGraw-Hill Book Company, 1980.[13] WILEY R G. Electronic intelligence: the analysis of radar signals[M].Second ed. Norwood,MA:Artech House,1993.[14] Analog Devices, Inc. AD9211 Datasheet[EB/OL]. 2007.[15] Xilinx, Inc. Fast Fourier Transform v6.0 [EB/OL]. 2008.