采用变压器模型的新型变压器保护原理及设计

在变压器差动保护中，如何区分励磁涌流与内部故障电流是一个固有的、不可回避的难题，多年来一直成为研究的热点。
   
现在实际运行的变压器差动保护，主要是采用以二次谐波制动原理和间断角原理来判别励磁涌流，其中二次谐波制动原理应用最为广泛。但是由于CT饱和，无功补偿用的并联电容或超高压长输电线分布电容的存在，使得变压器发生内部故障时也会产生很大的二次谐波，而且随着大型变压器铁心采用冷轧硅钢片后，饱和磁通倍数由1.4降至了1.2~1.3，甚至低至1.1~1.15，使励磁涌流的二次谐波含量有时低至10% 以下，这样二次谐波制动原理的制动比很难选取，保护就可能存在不正确动作；基于间断角原理的励磁涌流识别方案也存在着受CT传变影响等问题[1~4]。其他有代表性的鉴别励磁涌流的方法有波形对称原理、波形叠加原理、波形相关性分析法和波形拟合法。实际上，由于三相变压器励磁涌流的波形特征随系统电压和等值阻抗、合闸初相角、剩磁大小和方向、绕组接线方式和中性点接地方式、三相铁心结构、铁心材料和组装工艺、磁滞回线和局部磁滞环等不同而改变，所以任何以励磁涌流波形特征为依据的防止由励磁涌流而引起误动的措施均不能保证变压器差动保护不误动，差别仅是误动次数的多少[5]。
   
不依赖于励磁涌流波形特征的方案有：磁通特性识别法[6]，等值电路参数鉴别法[7]。这两种算法的不足在于都需要预先计算变压器漏感参数，而且整定困难，其应用前景取决于理论上的进一步突破[5]。本文利用变压器的原始正常模型，推导出了动作方程，并提出了保护判据。动模实验数据验证了该方案的正确性和可行性。

2  基本原理
   
如图1所示的双绕组单相变压器，下面的关系成立[8]：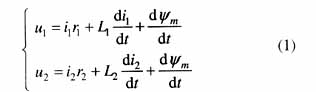



式中 U1、U2为一、二次绕组的电压；i1、i2为一、二次绕组的电流；L1、L1为一、二次绕组的漏感；r1、r2为一、二次绕组的电阻；Ψm为一、二次绕组的互感磁通。

设变压器的变比为nT=1。将式(1)中的dΨm/dt消去得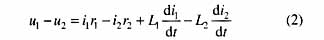





由于式(2)是根据变压器正常运行的模型得到的，所以它适合于外部故障、励磁涌流及过激磁情况。只有内部故障时，由于变压器模型本身的内部结构参数发生了变化，它才不再成立。因此，可以通过判别式(2)是否成立，来决定保护的动作行为，因而，在励磁涌流、过激磁、外部故障情况下保护不会误动作。下面分别推导两绕组和三绕组变压器的动作方程，并根据其动作方程提出了保护判据。

3 动作方程的推导

3.1两绕组三相变压器的动作方程[9]
   
由图2所示的Y/∆接线的三相变压器，根据电路原理可得到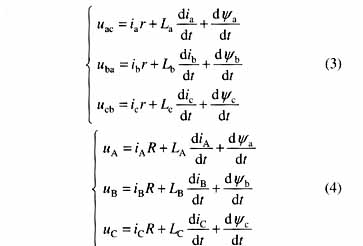


侧绕组各相的漏感；r为∆侧绕组各相的电阻；R为Y侧绕组各相的电阻；Ψa,Ψb,Ψc,为两侧绕组的互感磁链。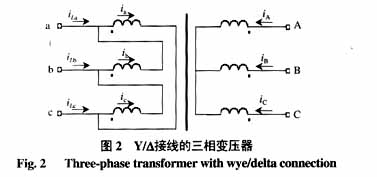





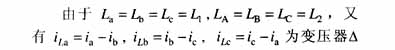
侧可测的各相电流，所以可将式(3)和式(4)中的等式分别两两相减，再进行合并，并归算到Y侧，可得


由于变压器制造厂家一般只提供变压器的短路电抗xk，并不提供各侧绕组的漏感L1,L2，可以利用关系式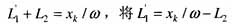代入式(5)，可得




在变压器正常运行(包括产生励磁涌流和外部故障）时，式(6)中的3个等式成立，而且3个等式中的L2应为同一值；只有变压器发生内部故障时，式(6)中的3个等式不成立，越严重的故障等式两边的差别就会越大，并且分别利用3个等式计算出的L2也会有较大差别。这是制定两绕组变压器保护判据的依据。

3.2三绕组三相变压器的动作方程

下面以Y0 / Y /∆-11接线的三绕组变压器为例推导动作方程，变压器接线图如图3所示。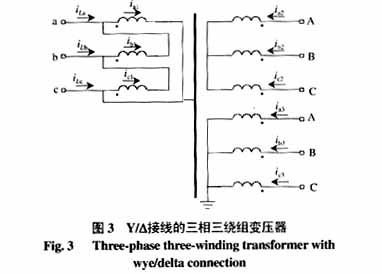



对单相绕组有：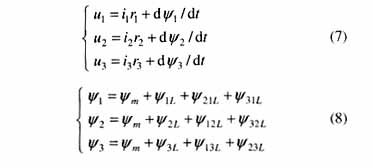

式中 r1,r2,r3为1、2、3侧绕组的电阻值;Ψ1,Ψ2,Ψ3分别为穿过1、2、3侧绕组的总磁链；Ψm为穿过1、2、3侧绕组的公共磁链；Ψ1L,Ψ2L,Ψ3L分别为1、2、3侧绕组产生的除Ψm以外的漏磁链；ΨijL(i≠j)为第i个绕组产生的除Ψm以外的和第j个绕组交链的漏磁链。
   
由式(7)、(8)可得A、B、C三相的关系如下：





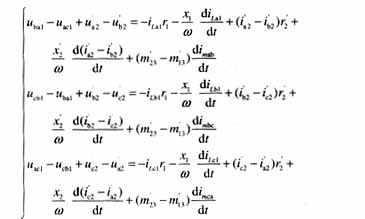
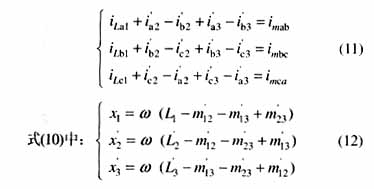
为变压器厂家提供的变压器各侧的电抗(归算到第1侧)。


4  保护判据
   
根据上面的推导，可以分别制定两绕组和三绕组变压器的保护判据。
   
（1）两绕组变压器的保护判据
   
判据1：当差动电流大于门槛值时，利用L2的估算值，计算式(6)中的3个等式两边的差值，如果等式两边的差值超过门槛值，判定变压器发生内部故障，保护跳闸。由于L2的估算值与实际值存在着误差，故此判据的动作门槛值要躲过励磁涌流和外部故障时方程两侧的差值，它能够保证在发生较严重的内部故障时保护正确动作。
   
判据2：当差动电流大于门槛值时，利用式(6)计算3个方程中的L2，如果3个方程分别计算出的L2之间的差值超过门槛值，判定变压器发生内部故障，保护跳闸。此判据可在判据1的基础上进一步判别变压器的轻微故障。但在内部相间短路时，由于差动电流数值很大，计算出的3个L2数值会较小，识别其差值较困难。
   
因此，判据1用来识别严重内部故障，判据2用来识别轻微内部故障，两者相结合就会达到很好的效果。


的6个方程等式两边的差值，如果等式两边的差值超过门槛值，判定变压器发生内部故障，保护跳闸。由于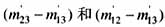的估算值与实际值存在着误差，故此判据的动作门槛值要躲过励磁涌流和外部故障时方程两侧的差值，它能够保证在发生较严重的内部故障时保护正确动作。


同样，判据1用来识别严重内部故障，判据2用来识别轻微内部故障，两者相结合会达到很好的效果。

5  动模试验及结果

5.1 动模试验系统

为了验证上述方法的正确性及可行性，通过动模试验获得了大量变压器在各种运行状态下的真实数据，在此，用这些数据对保护判据进行验证。
   
动模试验系统接线如图4所示。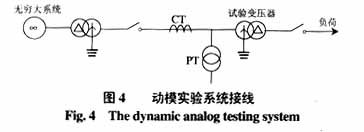



在此系统中的试验变压器为三单相变压器组Y,d11，单相变压器的参数分别为：额定容量10kVA；低压侧额定电压380V；低压侧额定电流25.3A；高压侧额定电压1000V；高压侧额定电流10A；空载电流1.45%；空载损耗1%；短路损耗0.35%；短路电压9.0%~15%。在进行数据录波时，每个采样周期采20个点。

5.2 试验结果

用动模试验中获得的数据来验证此方法的正确性，每种运行状态的数据分别测取10次。根据两绕组变压器的判据1，得到表1所示结果。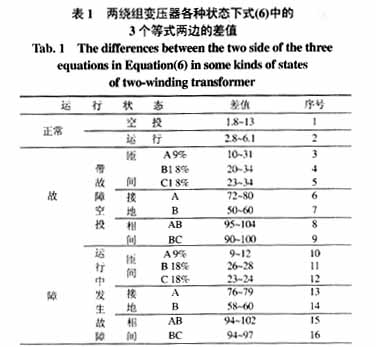



表1中的差值是10组数据差值综合结果，在计算中将L2估算为 (xk/w)/2。由表1可以看出，设判据1中差值的门槛值定为20，那么，除了轻微匝间故障无法识别外，其他故障均能够可靠地识别。
   
判据2可以对轻微匝间故障进行识别，下面依据判据2对表1中序号为1，3，10的3种情况进行判别。图5(a)、(b)、(c)是将动模试验数据代入到式(6)中，计算得出的3个等式中的L2的变化曲线。为了更加明显地比较3个L2的差别，图5(d)为计算出的3个L2的差值变化曲线。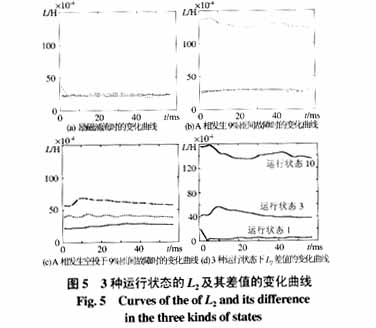



如图5(d)所示，励磁涌流时3个L2差别很小，而在内部匝间短路时其差别较大，可以利用判据2可靠地区分励磁涌流和轻微内部故障。

6  结论

该变压器保护方案是利用变压器正常运行时的模型来构成动作方程，由于只有在变压器内部发生故障时，本方程才不再成立，所以此方案不受励磁涌流的影响，并且在内部故障时有较高的灵敏度。该原理实现简单，避开了变压器难以取得的内部参数。仿真试验结果表明该方案能够可靠、迅速地切除变压器内部故障。