
摘要:这两年,化合物半导体的发展得到国家的大力支持,化合物半导体具有高的电子迁移率,高的反向击穿电压等特性,在移动终端上得到广泛的应用。而创建化合物半导体的器件模型,供集成电路设计者用于设计复杂集成电路,是集成电路代工厂的关键技术之一。化合物异质PN结,则是组成HBT的最基本结构,有必要系统地分析、创建PN结的电路仿真模型。经过几十年的发展,基于Si制程的PN结数学模型已经完善,但缺乏对化合物半导体的异质PN结模型的相关著述。基于Si制程的数学模型,应用到砷化镓制程,并用Verilog-A实现电路仿真模型的创建。最后,给出对应模型参数的提取方法,确保模型DC特性、RF特性的仿真结果跟实际测试数据高度一致。通过对砷化镓制程的PN结测量、建模,可以得出该Verilog-A模型的正确性、通用性。
关键词:半导体器件模型;集成电路;PN结;Verilog-A模型;化合物半导体
中图分类号:(O475) 文献标识码:A
引言
近年来,我国大力发展化合物半导体的制造技术。跟Si制程的BJT、CMOS相比,由于GaAs制程的HBT pHEMT具有高的电子迁移速率,高的击穿电压等特性,被广泛用来设计移动终端的PA、LNA。
PN结是半导体器件最基本的结构,是组成晶体管、场效应管等半导体器件的基本单元。因此,对化合物半导体的异质PN结的电性能特性的测量和建模就尤为重要。
本文的从PN二极管的物理结构、电特性测量、器件模型及其参数优化,最后到模型的比对展开,论述一个半导体器件建模的整个过程。
器件的数学模型,科学家们做了大量的研究,同时还在不断维护升级器件模型,使器件模型与不断升级的半导体工艺相匹配。不同的半导体制程,比如Si、GaAs、GaN等,PN结的模型仅仅是模型参数上的差别。因此,在模型参数的提取上,通常的做法是通过建模软件来调整参数,使得仿真曲线和测量曲线重合。考虑到二极管的数学模型的相对比较简单,本文将采用建模上的常规做法提取参数,顺便简单介绍数学分析的提取手段。
最后,是器件的数学模型到电路仿真模型的实现,本文采用语法灵活的Verilog-A语言来描述。并总结二极管建模过程中所需要经历的一般步骤。
1、PN结电性能测量
1.1 DC特性
使用半导体分析仪,测量PN结的正向和反向DC特性。
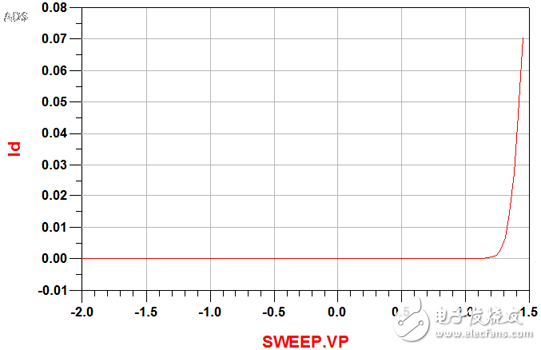
图1、二极管的DC IV曲线
1.2 RF特性
使用半导体分析仪和矢量网络分析仪组成的高频测量环境,测试CV曲线。
矢量网络分析仪设置固定频率110MHz,半导体分析仪扫偏压-2~1.45V;得到一组S_vs_V数据,转换成Y_vs_V,再经过数学变换: Zd=-2/(Y12+Y21),得到Zd_vs_V阻抗-偏压曲线,如下:
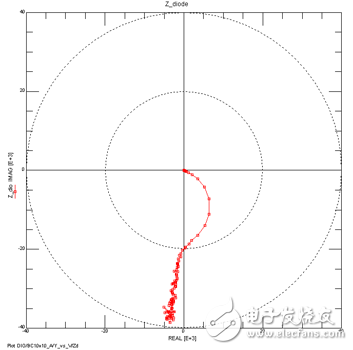
图2、二极管的Zd_vs_V/阻抗-偏压曲线
从图(2)可以得出,Zd的实部出现负值,等效为一个负电阻,这表明该PN结反向偏压的时候,在势垒区发生量子隧穿效应[1],即电子会越过势垒形成负电阻。
在结电容提取上,由于矢量网络分析仪的频率为110MHz,Zd的虚部近似为纯电容,因此有:imag(Zd)=-1/(2*PI*freq*C),经过换算可以得到C_vs_V曲线,作图如下:
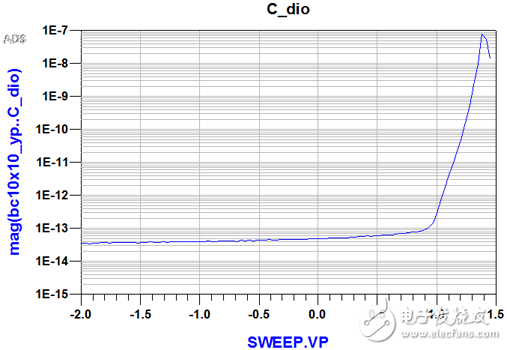
图3、二极管的CV曲线,对数坐标表示
2、数学模型
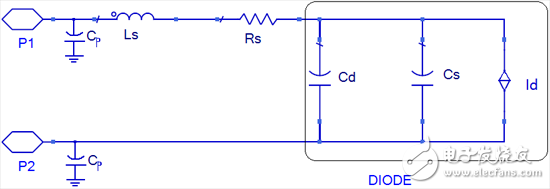
图4、小信号等效电路
其中,DIODE为内部本质二极管(Intrinsic diode);二极管的结电容由Cs、Cd组成。Ls、Rs为引线的寄生电感、寄生电阻。另,根据DUT的测试结构,二极管还存在一组对地电容Cp,上述变换过程得知,测量的RF CV曲线是由π型网络的Y12,Y21转换得来的,这组对地电容Cp对CV曲线不产生影响。
2.1 DC数学模型[2]
Id=:
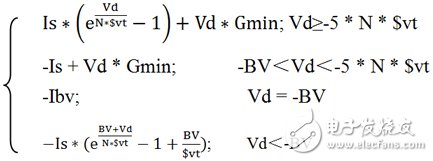
其中:
Is: saturaTIon current(leakage current);
N: emission coefficient(1≤N≤2);
BV: Breakdown voltage;
$vt=K * T/q;
Ibv=Is * BV / $vt;
2.2 RF数学模型[2]
关于结电容的模型,采用电量Q来描述。
当Vd<Fc*Vj时:
当Vd≥Fc*Vj时:
其中:
Vj: JuncTIon potenTIal
M: Grading coef
Fc: Forward bias junct parm
Fcp = Fc * Vj;
3、模型参数提取
DC参数提取
二极管开启电压附近,对数坐标表示的IV曲线是线性的,在这个线性区,Id的最后两项Is和Vd*Gmin对Id的贡献忽略不计,如图(4);因此,DC模型可以近似为:
两边取自然对数,则有:
ln(Id)=ln(Is)+Vd/(N*$vt)
得到一条新的曲线,从线性区的斜率可以提取到N,把线性区延伸到Vd=0的轴,可以提取Is。
接着,在大电流区域,做Rs的提取。
而建模上的做法是调整模型参数值,使得模型曲线和测量曲线重叠。如图:
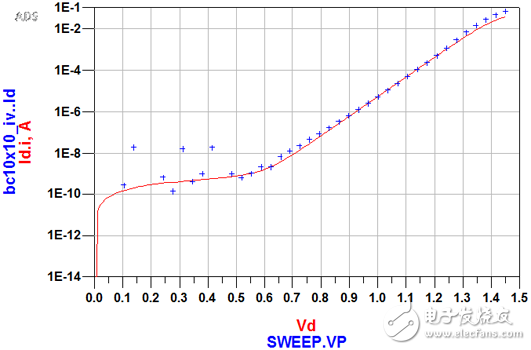
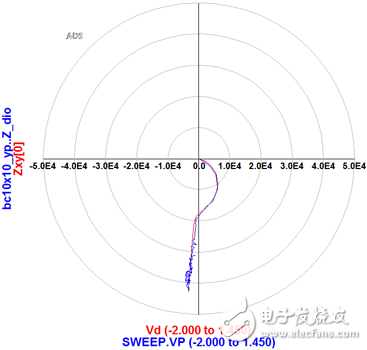
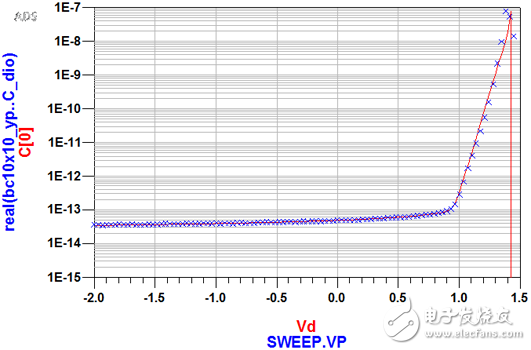
图5、参数提取
4、电路仿真模型创建
Verilog-A主要是描述组成电路网络的节点以及分支的电压和电流之间关系。图(4)的等效电路模型,要实现Verilog-A描述,除了本质二极管外,还需解决电阻,电感,电容元件。电阻性元件:V=R*I;电感性元件:V=L*ddt(I);电容性元件:I=C*ddt(V)。前两种是寄生参数的等效元件,为理想元件。但二极管的节电容C不再是一个常量,而是偏置电压Vd的函数,因此,要用电量Q来表示,即:I=ddt(Q)。
且有:
Q=Qs+Qd;
其中:
Qd由渡越时间参数决定:Qd=Tt * Id。从PN结的阻抗特性上看,渡越时间参数Tt贡献了一个负电阻,即PN结反向偏压的时候,电子的量子隧穿效应引起的[1]。
当Vd<Fc*Vj时:
上式,令
则,v=Vj*(1-u),有,=>
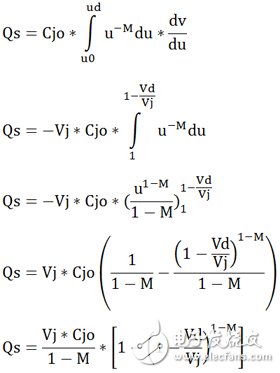
当Vd≥Fc*Vj时:
上式积分部分,令
则, ,有 ,

即:
根据上述公式,二极管的Verilog-A模型描述如下:
`include "disciplines.vams"
`include "constants.vams"
module PN_DIODE(anode, cathode);
inout anode, cathode;
electrical anode, cathode;
parameter real Area = 2; //Area scaling factor
parameter real Is = 1.2e-15; //SaturaTIon current [A]
parameter real Rs = 0.66; //Series resistance [Ohm]
parameter real Ls = 170e-12; // Series inductance[H]
parameter real N = 1.80; //Ideality
parameter real Tt = 1.2e-10; //Transit time [s]
parameter real Cjo = 2.3e-14; //Junction capacitance [F]
parameter real Vj = 1.06; //Junction potential [v]
parameter real M = 0.336; //Grading coef
parameter real Fc = 0.99; //Forward bias junct parm
parameter real BV = 25.45; //Breakdown Voltage
parameter real Gmin = 1.4e-9; //minimum junction conductance
real Vd, Id, Qd, Ibv;
real f1, f2, f3, Fcp;
electrical in1, in2;
analog begin
f1 = (Vj/(1 - M))*(1 - pow((1 - Fc), (1 - M)));
f2 = pow((1 - Fc), (1 + M));
f3 = 1 - Fc * (1 + M);
Fcp = Fc * Vj;
Ibv = Is * BV / $vt;
Vd = V(in1, cathode);
Id = I(in1, cathode);
// Intrinsic diode
if (Vd < -5 * N * $vt) begin
if (Vd == -BV)
I(in1, cathode) <+ -Area * Ibv;
else if (Vd > -BV)
I(in1, cathode) <+ -Area * Is + Vd * Gmin;
else
I(in1, cathode) <+ -Area * Is * (exp( -(Vd + BV) / $vt) - 1 + BV / $vt);
end
else
I(in1, cathode) <+ Area * Is * (exp(Vd / (N * $vt)) - 1) + Vd * Gmin;
// Capacitance (junction and diffusion)
if (Vd <= Fcp)
Qd = Tt * Id + Area * Cjo * Vj * (1 - pow((1 - Vd / Vj), (1 - M)))/(1 - M);
else
Qd = Tt * Id + Area * Cjo * (f1 + (1 / f2) * (f3 * (Vd - Fcp) + (0.5* M / Vj) * (Vd + Fcp) * (Vd - Fcp)));
I(in1, cathode) <+ ddt(Qd);
V(in2, in1) <+ I(in2, in1) * Rs;
V(anode, in2) <+ Ls * ddt(I(anode,in2));
end
endmodule
5、总结
本文中论述的是二极管的小信号模型,适用于半导体材料组成的PN结以及金属半导体组成的肖特基PN结。另外,论述的二极管的模型参数适用于GaAs HBT制程的Base和Collector材料组成的异质结。
参考文献:
[1] 刘恩科朱秉升罗晋生,半导体物理学[M]。电子工业出版社。
[2] Antognetti, Massobrio. model based on P-N junction theory[J].
[3] Franz Sischka, IC-CAP Modeling Handbook[M]. Agilent Technologies.
作者:邱文忠、李建勋、黄宏达,福联集成电路有限公司
作者简介
1,邱文忠、男、1984年出生于福建省莆田市;厦门大学本科学历,电子信息科学与技术专业毕业、中级电子工程师职称,从事砷化镓制程PDK开发工作。
2,李建勋、男、1961年出生于福建省晋江市;浙江大学本科学历,半导体器件专业毕业、高级电子工程师职称,从事砷化镓制程开发工作。
3,黄宏达、男、1968年出生于台湾彰化县;国立中山大学电机工程硕士学历,专长在CMOS工艺开发、器件设计;曾从事晶圆代工、设计服务、EDA软件。目前负责砷化镓HBT pHEMT工艺开发。
附录:
文章的创新点自述:完整论述了一个器件的建模过程,对器件的模型创建、参数提取有参考意义。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)