基于FPGA的压控晶振同步频率控制系统的研究与设计

高精度时间基准已经成为通信、电力、工业控制等领域的基础保障平台之一。时统设备通常采用晶体振荡器作为频率标准，但都由于晶振老化和温度变化等原因导致其频率长期稳定度差。随着GPS技术的发展和应用，利用GPS作为精确时间源的优良特性来同步本地时钟信息。但在实践中由于GPS提供的1pps信号经常受到干扰，如磁场干扰，多径误差等，造成误将干扰信号作为正常的1pps信号或GPS信号跟踪丢失等问题，导致测控系统出现误差过大现象，精度和稳定性难以保证。故1pps信号不能直接从GPS接收板作为精确的同步信号，必须通过技术处理，使其保持高精度和工作连续稳定性。目前针对上述问题文献多使用分立器件或单片机作为主控制器，需要添加外围时间间隔测量或鉴相等电路，不适宜用于压控晶振频率较高的场合。

本文是利用GPS提供的1pps秒脉冲信号，为解决上述问题，在FPGA（fieldprogrammablegatearray）的基础上利用干扰秒脉冲信号消除和偏差频率平均运算等方法，减少外围电路，既消减了GPS时钟信号的随机干扰误差，又消除了本地晶振时钟信号的累计误差，从而控制本地压控晶振输出频率，提高晶振的长期稳定性。

FPGA频率控制系统总体结构原理框图如图1所示。系统输入是GPS接收机在跟踪卫星时产生的1pps秒脉冲信号，逻辑电平输出，高电平持续时间为1.01±0.01ms，以高电平的上升沿作为秒脉冲信号输出的基准时间［9-10］。数字控制电路为FPGA控制电路，主控芯片为EP1C6-——144TQFP，可以反复软件编程，修改电路方案，外围硬件电路少，可靠性高。该电路将测量本地压控晶振产生同步秒脉冲与1pps秒脉冲之间的相位差，采用干扰秒脉冲信号消除和偏差频率平均运算等方法得到同步信号所需的相对频差。D/A转换器将相对频差转换为模拟控制电压，反馈到本地恒温压控晶振的控制端调整高稳晶振的频率信号，减小与1pps秒脉冲的同步相差，从而提高振荡器高频准确度和长期稳定性，实现数字同步时钟的驯服功能。

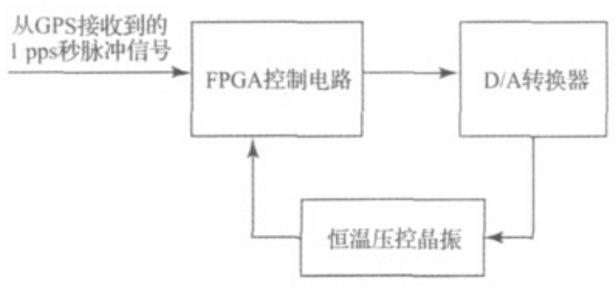
图1  FPGA频率控制系统总体结构原理

系统功能设计主要包含硬件设计和软件设计2大部分，如图2所示。软件实现部分为：以VHDL编程语言实现GPS信号对晶振的驯服功能，包括如何消除GPS干扰信号的方法，实现GPS同步时钟的方法，丢失GPS信号后继续对晶振频率的驯服控制，以及输出本地同步秒时钟信号。硬件实现部分为：D/A转换器提供转换后的模拟控制电压，恒温压控晶振根据模拟电压校准频率，并反馈回FPGA处理器。

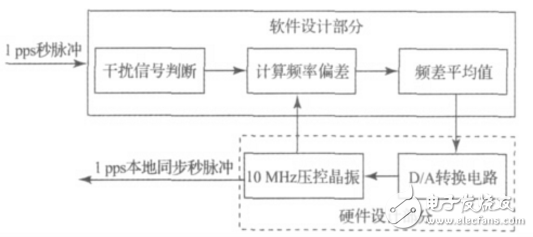
图2  系统功能设计

1pps秒脉冲信号以方波形式输出，高电平表示有秒脉冲输出，高电平脉冲宽度不是恒定值，持续时间约为1ms，有0.01ms的误差，这就导致在1pps信号高电平期间的晶振计数值不相等。另外由于干扰，接受到的1pps信号中有干扰脉冲信号，若把干扰脉冲上升沿作为1pps信号的上升沿开始计数，计数结果必然不准确，所测得的晶振频率值与实际值偏差过大。需要软件判断出干扰信号并作出处理。

数字电路中干扰脉冲的高电平持续时间多数是微秒级，很少有超过1pps秒脉冲信号高电平持续时间的，因此以秒脉冲高电平持续时间作为判断依据，以本地压控晶振计数来实现计时功能。晶振标称频率是10MHz，2ms的计数值理论值为20000。在晶振高频脉冲输出事情发生clk‘eventandclk=’1‘的前提下，遇到1pps信号事件sclk’eventandsclk=‘1’开始计数，同时用寄存器counter4保存计数值，如超过2ms高电平的脉冲信号为正常1pps信号，若小于2ms则认为是干扰信号，寄存器counter4计数值返回至该信号脉冲上升沿前的计数值。

为了校准晶振输出信号频率，需要将频率偏差值计算出来，计算出对应调整数值，通过D/A转换器变为模拟电压，并反馈给恒温压控晶振，以此达到调整的目的。可以用一元二次回归模型对输出的晶振秒时钟与GPS秒时钟的频率偏差进行分析。

由于本地恒温压控晶振短期稳定度高，小于1×10-10/s，可以不考虑晶振秒脉冲的随机误差，只考虑累积误差产生的频率偏差及线性漂移误差，晶振分频秒时间序列的第x个秒时钟的时间误差e（x）为：

e（x）=a+bx+cx^2（1）

式中：a为秒时间序列的初始误差，b为频率偏差的误差系数，c为频率线性漂移的误差系数。

通过一元二次回归分析可得式（1）的晶振误差估计值服从正态分布：

^e（x）=^a+^bx+^cx2～N（a+bx+cx2，D（^e））（2）

根据回归分析，可得，当x=n时，秒时钟的时间误差的方差有最大值Dmax。通过分析上式最大方差Dmax与回归分析样本数n之间关系得，样本数n越大，最大方差Dmax越小，也就是晶振分频秒脉冲与GPS秒时钟的偏差越小。但样本数n不能取无限大，受FPGA软硬件资源的限制，一般来说，当n≥3时，调整后的晶振分频秒脉冲的时间偏差小于GPS秒时钟的偏差，可以满足要求。

上述方法需要在1s内累积晶振计数值，需要有24位的寄存器存储计数值，对芯片运算处理速度要求过高，且占用较多FPGA资源，影响控制速度。在此基础上，本文采用偏差频率平均运算的方法。即将每s内晶振分频秒脉冲与GPS秒时钟偏差值求出，每3个样本时间作为控制的循环周期，3s累加内总偏差值为Z=Z1+Z2+Z3，求得循环周期平均偏差值Z0=Z/3，在下一循环样本周期内，每秒反馈给晶振，调整晶振输出频率。

晶振分频秒脉冲与GPS秒时钟偏差值具体方法为：用寄存器counter1存入每s内晶振的计数值，理论计数值为1×107个晶振脉冲。寄存器counter2为秒时钟计数器，当判断1pps信号为非干扰信号后，寄存器counter2自加1计数。正常秒脉冲频率的偏差值在±128范围内，超过范围则是超差信号，不作处理，故利用寄存器counter1的低8位作为误差频率的寄存器counter3。当counter2值达到循环控制样本数3时，做平均偏差频率计算，结果存入寄存器——counter7输出。

方案仿真波形如图3所示。因理论计数值较大，实际程序运算时间过长，结果难以清楚观察，对1个秒脉冲时间内的晶振脉冲数减小，为15个晶振脉冲。数据减小不影响方案的验证。可以看出，在counter2寄存器计数到3个秒脉冲的1个控制循环周期内，低8位的频率平均误差为15，counter7寄存器得到的余数也为0001111。结果表明该方案可以准确得到频率偏差值。

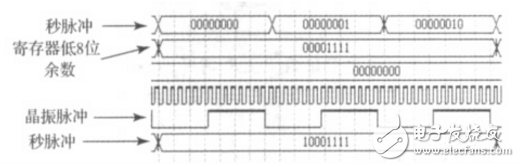
图3  方案仿真波形