大神教你：FIR与IIR低通滤波器的最简最快实现

在设计单片机程序的过程中，经常需要利用ADC采集外界模拟信号。有一些信号我们比较关注它的直流与低频分量，希望将高频噪声滤除，就需要借助低通滤波器。

低通滤波器常见的利用电子电路实现的方式是一阶RC无源滤波器。简单讲就是这样：

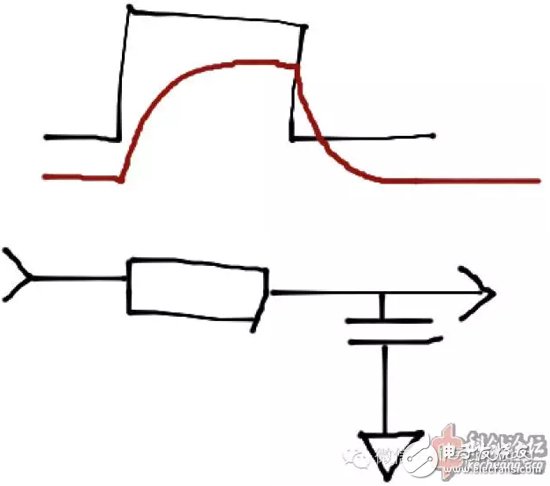
RC滤波器的各类计算略，有需要请谷歌。

RC滤波器用于单片机ADC输入有许多缺点。如果R的取值较小，就要求C较大，同时输入信号阻抗不能过大；如果R的取值较大，则ADC采样瞬间释放的电荷会使得端口电压升高而无法在采样时间内释放到稳定水平。这会导致采样精度问题。

而即便使用一个运放来缓冲RC滤波器的输出，再接入ADC，也只解决了输入阻抗问题，ADC电路受外界干扰仍然会在转换结果中产生噪声。因此，我们希望在单片机内部利用程序来实现低通滤波，彻底摆脱高频噪声。

数字低通滤波器有两种形式，IIR和FIR。

IIR是无限脉冲响应滤波器，它的特点是输出与无限久以前的输入有关。这就如同上面RC滤波器的响应，随着时间流逝，输出电压只会无限接近于输入电压，而不会等于。

用c语言实现IIR低通很简单：

int last = 0;

//下面的函数以固定频率运行，函数输出就是IIR低通滤波器的输出。

int lowpass（）

{

int this = ADC（）;

last = （this * 1 + last * 15） / 16; //新的last 是旧的last * 15 / 16 + this * 1 / 16

return last;

}

如果对函数返回值作图，得到的波形就会和RC滤波器的波形一样。要改变截止频率，只需要改变函数第二句中新的last的组成（例如改成3/4和1/4，截止频率会提高）。

值得注意的是，上述代码使用了整数乘法和2的n次幂除法，因此编译优化后，在8位平台上运行超快。如果你使用带有浮点运算模块的平台，请直接使用浮点数。

IIR的特点是节省内存，上面的滤波器只使用了两个变量。

IIR的缺点是不稳定。如果你把15改成17，显然这个滤波器的输出会在一段时间后溢出。你必须负责保证IIR滤波器稳定。

FIR是有限脉冲响应滤波器，它的特点是输出与有限久以前（一段时间内）的输入有关。由于数字系统中采样是离散的，每一段时间内的采样数是固定的，所以FIR滤波器的每一个输出值，可通过对之前的若干个数量固定的采样值进行计算得到。特别是，因为对固定数量的采样值的计算在FPGA电路中可以并行实现，因此FIR滤波器常常被用于基于FPGA的数字信号处理系统。相对的，IIR滤波器不依赖之前的采样，但依赖于之前的滤波器状态（存在反馈），因此在大部分比一阶低通滤波器复杂的应用场合，IIR滤波器的各项特性没有FIR稳定（若要实现稳定，对计算精度要求较高），而且计算起来比FIR要慢，设计上也没有通用性。

下面我用c语言实现一个最简单的FIR低通。我们将最近的8次采样值加起来，求平均值，作为输出。

int buf［8］;

int lowpass（）

{

int k = 7;

while（k--）

buf［k］ = buf［k-1］; //将buf［6］ 移到buf［7］， buf［5］ 移到buf［6］，等等，以空出buf［0］

}

buf［0］ = ADC（）;

return （buf［0］ + buf［1］ +.。.+ buf［7］） / 8;

}

这个滤波器的时域图像有点像这样：

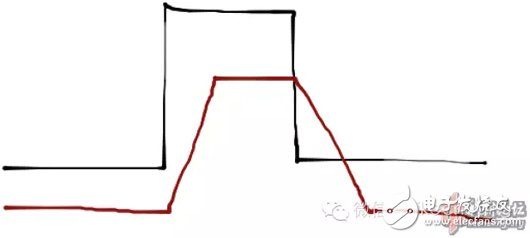
值得注意的是，上面这个函数可以被进一步简化，以加速计算。上面这种滤波器有另一个名字：滑动平均滤波器，这个滤波器大部分股民应该很熟悉。

虽然时域图像很美观，但是这个滤波器的频域图像一点也不美观：

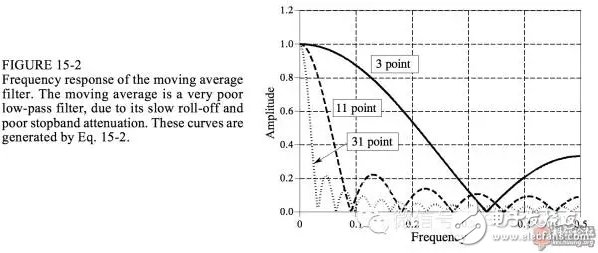
可见，随着点数的增加，图像看起来只是从右向左缩水，对高频的抑制并不好。

所以如果想要获得比较好的低通效果，不应该增加点数，而应该将多个一样的FIR滤波器串联使用（一个的输出作为下一个的输入）。

注：pass是“遍”的意思，表示迭代次数。

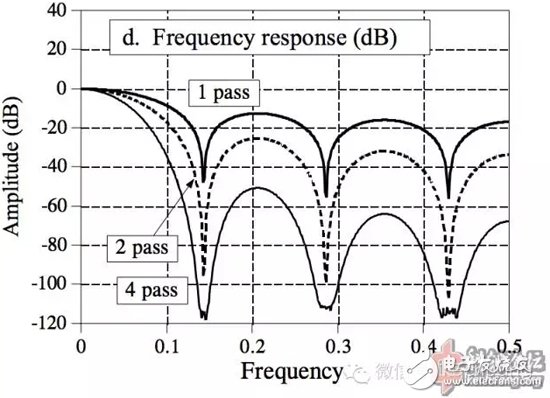
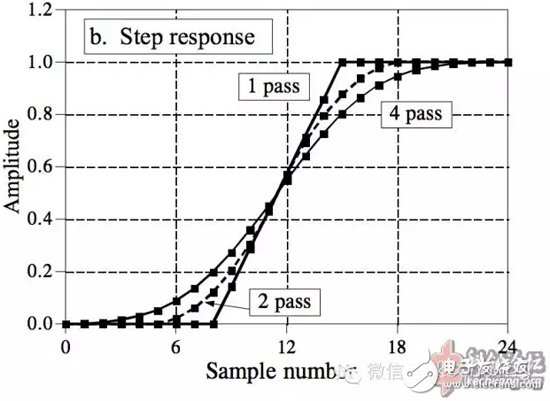
上面是串联使用的幅频响应。而时域图像也很美观：

结尾给出的是写这篇文章时随手找到的资料。大家一定要学会使用谷歌搜索英文关键词，因为老外比我们对待知识的态度更严肃也更开放。

刚才的滑动平均滤波器，时间复杂度是O（n）（设每次处理n个采样）。

可以优化为O（1）的形式：

int buf［8］;

int k=0;

int result=0;

int lowpass（）

{

result -= buf［k］;

buf［k］ = ADC（）;

result += buf［k］;

k = （k + 1） % 8;

return result;

}