
作为电子工程师,在职业生涯中会碰到各种各样的问题,其作用就是利用所学的知识解决各种问题。当进行以电流形式输出的传感器电路设计时,通常会通过以下的步骤进行设计:首先电流转换为电压,然后进行电压变换使其适合MCU处理的电压范围。从上面的步骤看出电流转换电压是电流形式输出传感器设计的一个重点。下文将从简单到复杂进行电流转电压电路的分析。
首先,看下经典的电流转换电压静电电路,通常使用一个运放和一个反馈电阻进行设计,如下图所示:
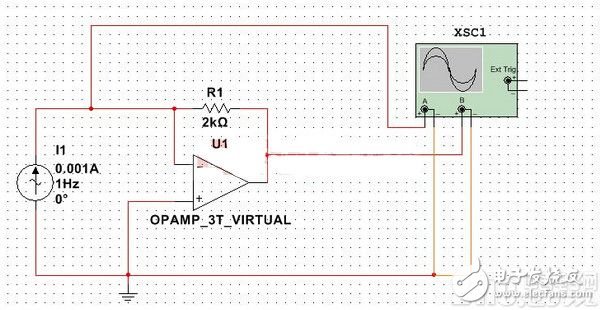
当设置输入电流源为1Hz电流强度为1mA时,在mulTIsim上仿真结果如下:
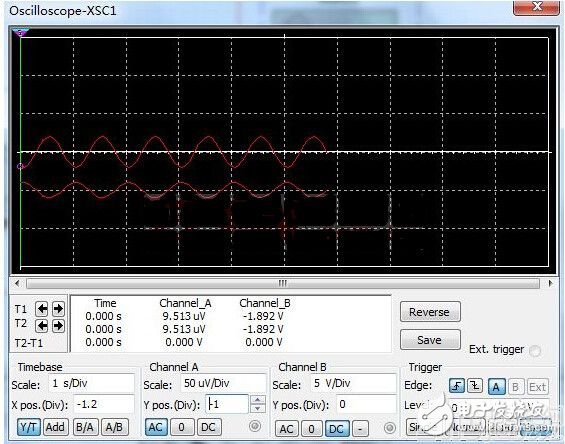
从仿真的结果上可以看出,该电路完成了电流与电压的转换并进行了信号的放大。虽然完成了设计的初衷,当深入的分析一下,会有另一番风景。
在电流转换电压电路中,一个重要的参数就是灵敏度,如上图,经过一个运算放大器将0.001A的电流转换为2V的电压,就可以定义该电路的灵敏度为2V/ma,也就是说电流转换电压的电路,输出电压大小与电路的灵敏度有关。
上图的电流转换电压电路的反馈元件是电阻,而实际上,可以采用电阻、电容和电感的各种组合,其一般的表达式为:
Vo(s)=-Z(s)*Ii(s)
在实际使用时,有的时候需要高灵敏度的电流电压转换电路,如果按照上图的电路进行设计,采用大点的反馈元件即可,但是这也为后续的设计和方案的一致性埋下了失败的伏笔:反馈元件数值越大,如果精度相同,那么一致性会大打折扣。比如对于上面的电路,采用5%的1kΩ的电阻,其有效值范围为950-1050Ω,如果换为1MΩ的5%的电阻,其有效值范围为9500-10500Ω。为了解决类似的问题,在实际的设计中会采用T型反馈网络的电流电压转换电路,如下如
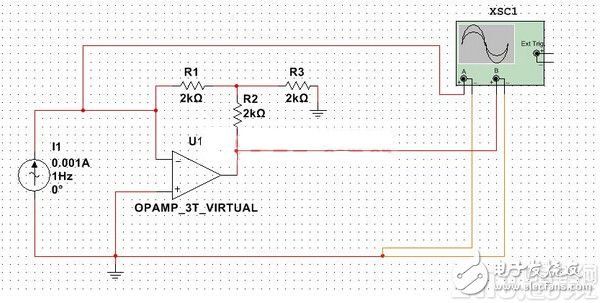
利用基尔霍夫电流定律,可以求得
Vo=-(1+R2/R1+R2/R3)*R1*I(i)
这样,就可以利用数值较低的元件完成灵敏度较高的电流电压转换电路。利用mulTIsim仿真结果如下:
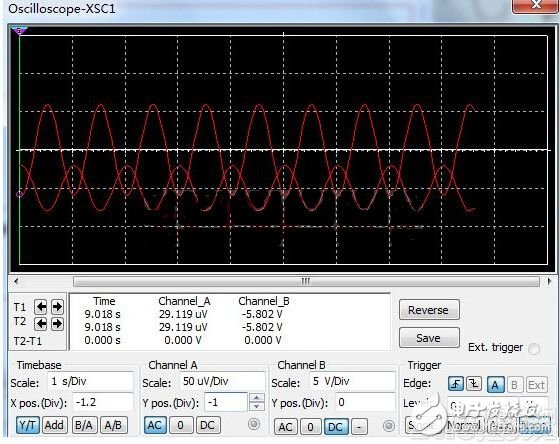
除了在饭反馈网络上下功夫,还要考虑另外一个因素:运放的输入偏置电流。
所谓的输入偏置电流就是保证放大器工作在线性范围,为放大器提供直流工作点的电流。对于采用三极管作为运放输入极的运放来说,输入偏置电流就是基极的电流。如果设计高灵敏度的电流电压转换电路,并且需要高的输入电阻,这时可以考虑用 JFET 输入或者MOSFET输入的运放。因为 JFET 是电压控制器件,其输入偏置电流参数是指输入 PN 结的反向漏电流,数值应在 PA 数量级。电压控制的MOSFET 器件,可以提供更小的输入漏电流。
一个常用的电流电压转换电路应用例子就是光电探测电路。相信做过光电检测的人对该电路一定不会陌生。另一个常用的电流电压转换电路就是经典的R-2R梯形DAC电路。具体电路设计如下:
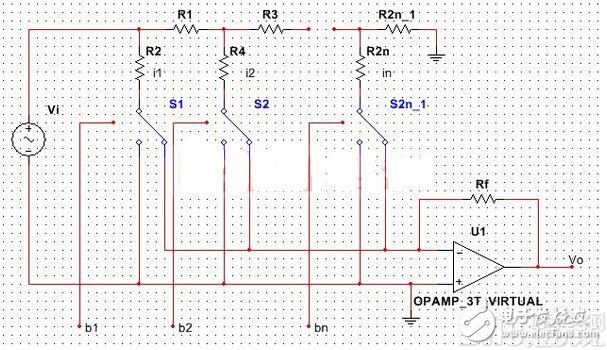
该电路中,可以通过bn的数值进行开关Sn的开关状态,
在该电路中,奇数项电阻阻值为R,偶数项电阻阻值为2R,此时
Vo=-(Rf/R)Vi(b1*2-1+ b2*2-2+ …+ bn*2-n)
现在深入的分析运放U1的两个输入端电流和,将电源Vi和所有的权电阻和开关看做一个黑匣子,利用基尔霍夫电流定律可知,运放的N和P极的电流在数学表达上可以表示为
In+Ip=(1-2-n)Vi/R
在数字电路中可以表示为两个状态的互补形式。
R-2R梯形DAC电路的优点是设计简单,且每位权电压变化最小。但是,也有其设计的难点:运放的N极和P极电压必须最大限度的接近,否则容易产生线性误差,这在一定程度上影响了DAC的精度。为尽量减小这一误差,在实际的设计中经常采用低漂移量的运放和在设计使总输入失调误差最小。
电路设计本身就是一个技术和艺术的结合,也是一个由浅入深的经验过程,上面的小文是笔者在电路设计中碰到的和解决问题得出的一些浅见,如有不当和解释不详的情况,请留言,共同提高。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)