
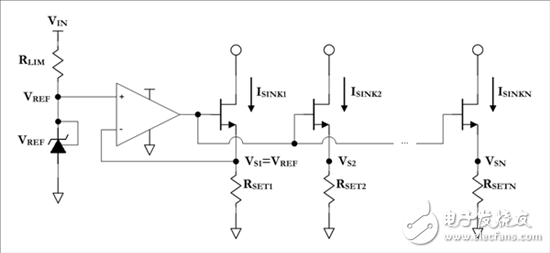
图1:灌电流网络
该等式如下所示:
现在,关于等式1,有什么可说的呢?首先,MIN比为1时,相应的MRN比也将为1,这恰如预计的一样。第二,MIN大于1时,等式1分母中两个项具有不同的表现。这意味着基于某些相关物理量(Kn、RSET1、VREF)的取值,MRN可以变得任意大。因此,应避开这一范围,相应地,应转向MIN ≤ 1区域,即确保ISINKN小于或等于ISINK1,N取任意值。
注意,等式1中根项的分母(Kn、RSET1、VREF乘积)在MRN与MIN1:1线性关系中可导致结果变得极大。最终,VREF和RSET1可增大该乘积结果的可用范围值将受相应的沉余量所限制,不过值得注意的是,ISINK1值固定时,增加VREF需要同时增加RSET1。乘积中最后一个变量Kn是MOSFET过程跨导,可通过设备的选择使其最大化。Kn针对MRN与MIN线性关系(50个Kn取值)的影响见以下图2所示。
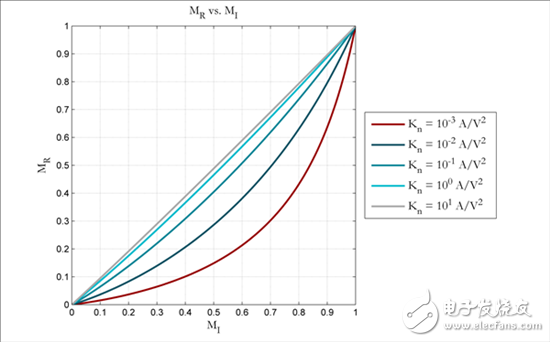
图2:过程跨导电阻比vs电流比
过程跨导的命名是基于其对所有材料与工艺过程属性如载流子迁移率、氧化物介电常数和氧化层厚度(μ、εox、tox)的依赖:
不过,它也依赖于设备的W/L比,所以在一般较大的设备中,等式1将表现出更为突出的线性行为。虽然大多数数据资料中不包括Kn,但它可以从一个普通的参数计算而来,这个参数是向前跨导,往往记作gm或gFS:
回想一下饱和区工作的NMOS漏极电流等式为:
忽略通道长度调制并调整方程4的项后,可得出:
将结果代入等式3,最终得出Kn:
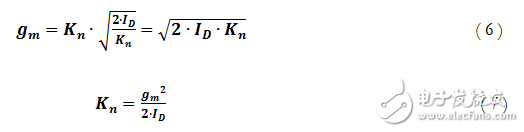
因此运用等式7可为偏置网络选择最优的MOSFET设备。此外,获得该值后,可用于等式1以(更准确地)计算出所需RSETN电阻值,从而生成所需ISINKN电流。
须重点注意的是,等式1倾向于高估MIN≤1区域的RSETN电阻;也就是说,这会导致电流低于所需值。然而理想的晶体管(MIN=MRN)总会使这一区域的RSETN电阻被低估。因此,计算这两个值将最终限制住所需的确切值。两个随机选择的NFET、2N6755和IRFZ40,其中列出了gFS分别为5.5A/V2(ID= 9A)和15A/V2(ID=31A)。假设用以实施的MIN比为¼,用等式1计算纠正的RSETN和MRN比值(以及一些简单的设计值),结果如下面表1所示。
表1:电路参数和计算出的RSETN和MRN(MIN=¼)
利用以上所列有关IRFZ0晶体管的情况,图3显示的是TINA-TI图1电路模拟的结果,RSETN值的计算基于理想状态(这类状态下为5Ω)、纠正状态(等式1)以及两者平均的状态。
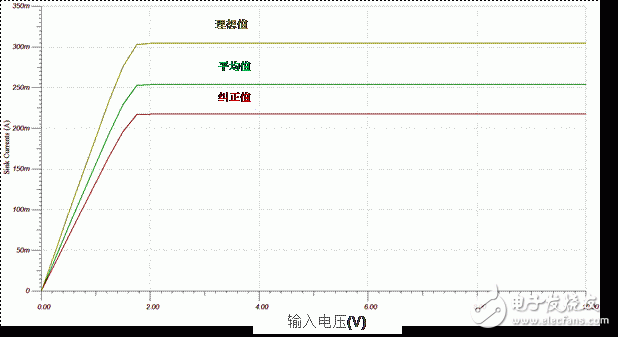
图3:理想、纠正与平均RSETN值下的灌电流vs漏极电压
使用2N6755和IRFZ40两者进行模拟的结果以及RSETN的三个不同取值经汇总后见以下表2,其中已计算出百分误差。
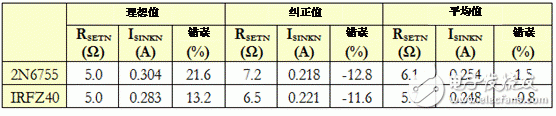
表2:RSETN计算方法与相应准确性
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)