opencv如何实现图像旋转_原理是什么

　　旋转一般是指将图像围绕某一指定点旋转一定的角度，图像旋转后会有一部分图像转出显示区域，可以截图那部分，也可以改变图像的尺寸使得图像显示完全。

　　图像旋转原理

　　所谓图像旋转是指图像以某一点为中心旋转一定的角度，形成一幅新的图像的过程。这个点通常就是图像的中心。

　　由于是按照中心旋转，所以有这样一个属性：旋转前和旋转后的点离中心的位置不变。

　　根据这个属性，可以得到旋转后的点的坐标与原坐标的对应关系。

　　原图像的坐标一般是以左上角为原点的，我们先把坐标转换为以图像中心为原点。假设原图像的宽为w，高为h，（x0，y0）为原坐标内的一点，转换坐标后的点为（x1，y1）。可以得到：

　　X0’ = x0 -w/2;

　　y1’ =-y0 + h/2;

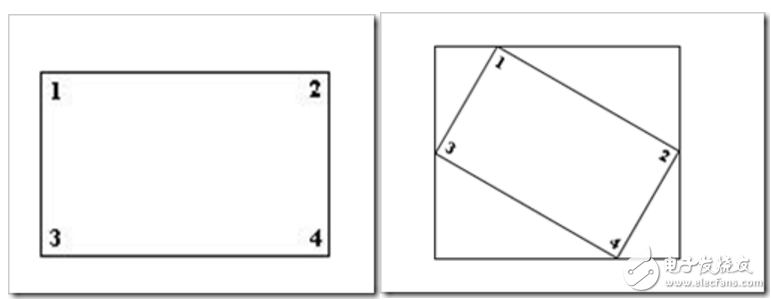
　　在新的坐标系下，假设点（x0，y0）距离原点的距离为r，点与原点之间的连线与x轴的夹角为b，旋转的角度为a，旋转后的点为（x1，y1）， 如下图所示。

　

　　那么有以下结论：

　　x0=r*cosb；y0=r*sinb

　　x1 = r*cos（b-a）= r*cosb*cosa+r*sinb*sina=x0*cosa+y0*sina；

　　y1=r*sin（b-a）=r*sinb*cosa-r*cosb*sina=-x0*sina+y0*cosa；

　　得到了转换后的坐标，我们只需要把这些坐标再转换为原坐标系即可。

　　x1’ = x1+w/2= x0*cosa+y0*sina+w/2

　　y1’=-y1+h/2=-（-x0*sina+y0*cosa）+h/2=x0*sina-y0*cosa+h/2

　　此处的x0/y0是新的坐标系中的值，转换为原坐标系为：

　　x1’ = x0*cosa+y0*sina+w/2=（x00-w/2）*consa+（-y00+h/2）*sina+w/2

　　y1’= x0*sina-y0*cosa+h/2=（x00-w/2）*sina-（-y00+h/2）*cosa+h/2

　　=（y00-h/2）*cosa+（ x00-w/2）*sina+h/2

　　在OpenCV中，目前并没有现成的函数直接用来实现图像旋转，它是用仿射变换函数cv：：warpAffine来实现的，此函数目前支持4种插值算法，最近邻、双线性、双三次、兰索斯插值，如果传进去的参数为基于像素区域关系插值算法（INTER_AREA），则按双线性插值。

　　通常使用2*3矩阵来表示仿射变换：

　　

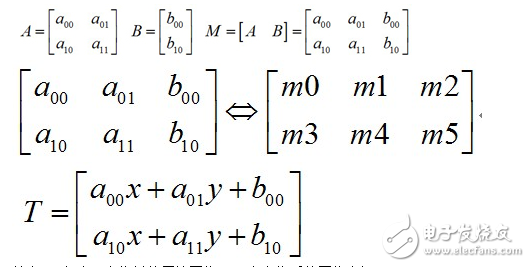
　　其中，T相当于变换前的原始图像，x，y为变换后的图像坐标。

　　对于cv：：getRotaTIonMatrix2D函数的实现公式为：

　　

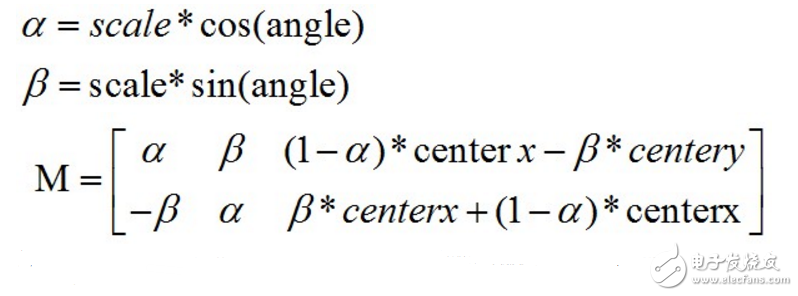
　　其中scale为缩放因子（x、y方向保持一致），angle为旋转角度（弧长），centerx，centery为旋转中心。