
还记得加法器吗?我们曾在第三章中提到过。还没看过的可以戳这里。上次只讲了行波进位加法器,还曾说过有机会要再讲讲超前进位加法器。这不,机会来了。我们今天就来讲讲上次略过的超前进位加法器。
行波进位加法器和超前进位加法器都是加法器,都是在逻辑电路中用作两个数相加的电路。我们再来回顾一下行波进位加法器。行波进位加法器的设计思路其实和我们做加法计算的思路一致:从个位开始,将两数相加的本位写下,将进位写在下一位。然后十位看看上一位的进位和两个加数的十位数字,再将两数相加的本位写下,将进位写在下一位。以此往复,算出全部的位数,得到最后的结果。以三位加法器为例,具体过程如下图所示。
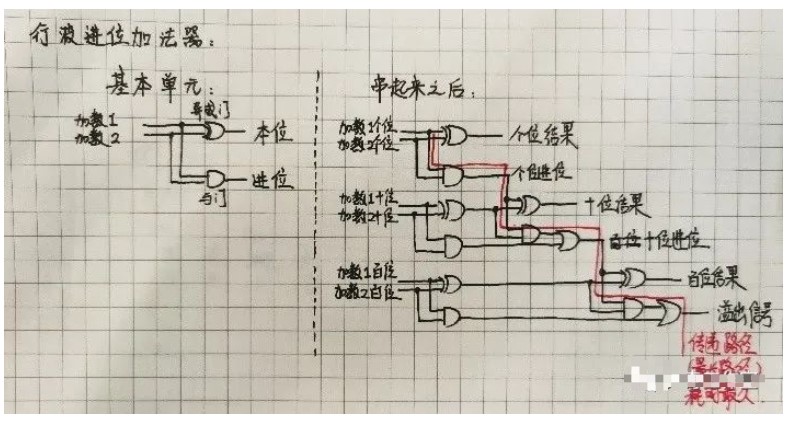
行波进位加法器
我们会发现一个问题,如果要算出十位的数值,我们得把个位的进位先算出来。同理,要算出百位、千位、万位都要先把前面的进位算出来。好像没什么问题对吧?但是现在的CPU里的加法器动辄32位以上,如果要一位一位地计算出结果,至少要60多级(没仔细算)的逻辑门,这样运算速度太慢了。人们就在想能不能直接先把后面的进位整出来,这样就不用等前面的运算逻辑了。听起来很玄乎:不先算前面的数字怎么可能把后面的进位整出来?
其实道理很简单,就是用空间换时间。以百位为例,如果百位的运算电路直接知道个位和十位的数字,那么百位的逻辑电路是不是就能直接判断出十位给百位的进位?有人会问:“不对啊!你百位的电路不也得把个位和十位加加看才能知道十位给百位的进位的吗?那和之前的电路不是一样的吗?”问题就出在这了,一样吗?如果说之前的行波进位加法器是做加法运算做出进位来的,这个过程需要时间,那么超前进位加法器更像是直接死记硬背答案的,很快就能做出反应。举个例子01+01,行波进位加法器会从个位开始算,个位是0进位1,十位是1进位0,计算完毕。而超前进位加法器则是说“啊!我记得这个组合,给百位的进位是0“。看到了吗?超前进位加法器气都不带喘的直接吐出答案了,这暗示我们考前背背答案有些时候是有点用的
言归正传,超前进位是如何实现记忆的呢?可以看这张超前进位的“记忆”电路图,其实质是将输入组合和输出写死在逻辑门里了。通过前几位的数字直接将进位输出了,所以我们完全可以直接让电路将答案背住,这样甚至不需要再进行一次加法,电路逻辑还被化简了。
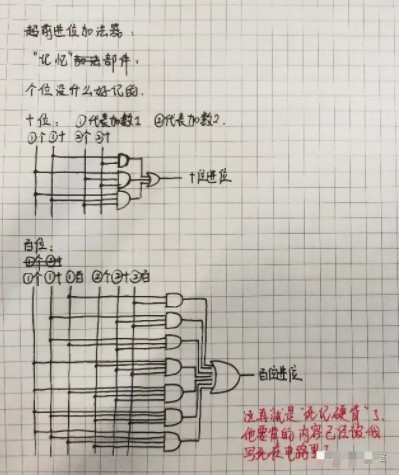
进位“记忆”
但是还有问题,如果直接背答案的话,即使是四位的加法器也会很复杂,可以看上面那张图,只是百位的进位就已经如此复杂了。有没有什么办法简化一下电路呢?有!我们可以再用时间去换空间。当然不是像行波进位加法器那样把所有的时间都拿去换了空间,而是有选择地拿一部分时间来换空间,达到时间和面积的平衡。
具体怎么做呢?我们把每一位数的两个数字直接做运算,得出每位上的和与进位,比如110+011的和就是101,进位就是010。然后再根据每位的和与进位得到最终的进位。这样的设计极大降低电路复杂程度,但同时,时延也增加了。什么道理呢?简单提示一下:比如百位什么时候会有进位?百位自己有进位、十位有进位且百位和是1、个位有进位且十位和是1且百位和是1。相信我这么一说,你们能直接把电路画出来了。(滑稽)
那难道就结束了吗?如果这样,第三十二位的逻辑是不是有点复杂?那咋办?解决办法也很简单,我们先四位四位地加或者八位八位地加,最后把结果再放一起再超前进位加一遍就好了,这样就不会出现上面那种情况,逻辑门的数量和级数都能得到最好的平衡。
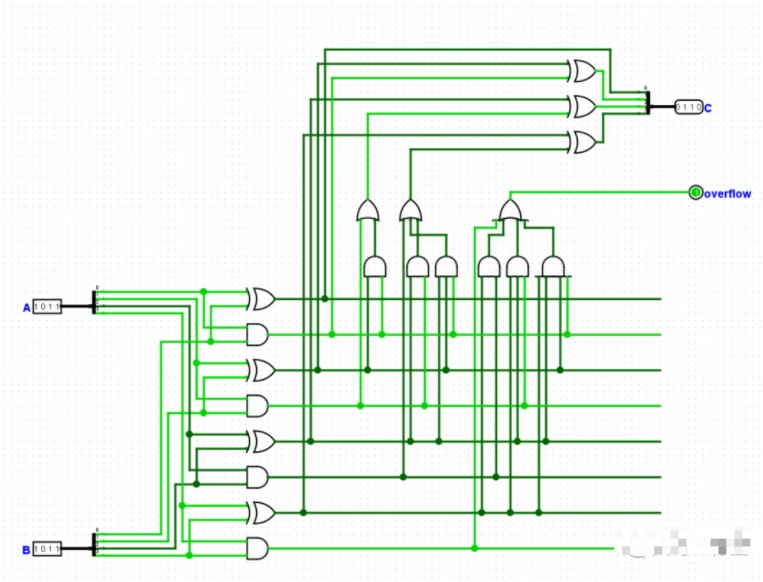
最后上一张超前进位加法器的全览图。(比较懒,只做了四位的,反正道理都一样)
审核编辑:刘清
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)