设X~N(μ,e^2),称Y=e^x所服从的分布为对数正态分布,试求Y的概率密度函数

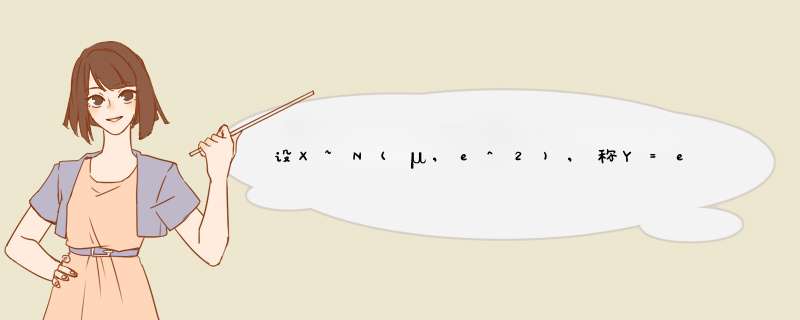
解；(x-u)/e~N(0,1)

fx(x)=φ((x-u)/e)/e

FY(y)=P(Y<=y)=P(e^X<=y)=P(X<=lny)=FX(lny)

fY(y)=FY(y)'=fX(lny)/y=φ((lny-u)/e)/(ey),

如有意见，欢迎讨论，共同学习；如有帮助，请选为满意回答！

%生成1e6个均值为1、方差为2的对数正态分布的随机数N=1e6;m=1;v=2;mu=log((m^2)/sqrt(v+m^2));sigma=sqrt(log(v/(m^2)+1))[M,V]=lognstat(mu,sigma)X=lognrnd(mu,sigma,1,N);

当对数函数的底数大于0小于1时，函数图像过点（1,0），从左向右逐渐下降，从右向左逐渐逼近y轴。

当对数函数的底数大于1时，函数图像过点（1,0），从左向右逐渐上升，从右向左逐渐逼近y轴。

关于“不同底数的图像间关系”，给你个判断方法：作直线y=1，看它与对数函数图像交点的横坐标（就是对应的对数函数的底数）的大小。

历史：

纳皮尔对数值计算颇有研究。他所制造的纳皮尔算筹，化简了乘除法运算，其原理就是用加减来代替乘除法。 

他发明对数的动机是为寻求球面三角计算的简便方法，他依据一种非常独等的与质点运动有关的设想构造出所谓对数方法，其核心思想表现为算术数列与几何数列之间的联系。在他的1619年发表《奇妙的对数表的描述》中阐明了对数原理，后人称为 纳皮尔对数，记为Nap，㏒x。

lnX ~ N(1, 4^2)

P(1/e≤X ≤ e^3)

=P(-1≤lnX ≤ 3)

=P[(-1-1)/4 ≤ Z≤ (3-1)/4)

=P( -1/2 ≤ Z≤ 1/2 )

查表！

常见的离散型随机变量的分布有单点分布、两点分布、二项分布、几何分布、负二项分布、超几何分布、泊松分布等

常见的连续型随机变量的分布有：均匀分布,正态分布、柯西分布、对数正态分布、指数分布、伽玛分布、贝塔分布、学生分布等等