已知Ackerman函数定义如下：

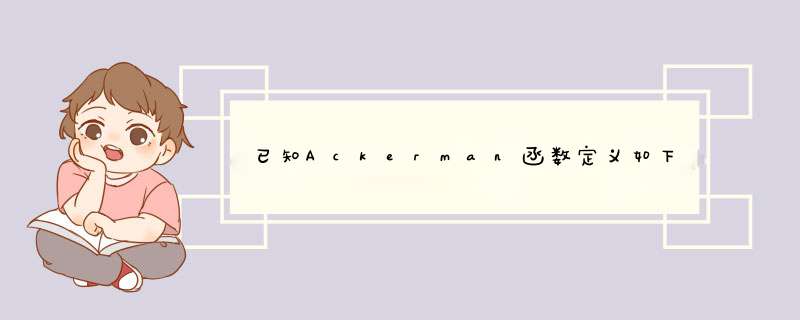
//（1）递归算法如下： 

int akm(int m,int n)

{//递归设计

 int r,g;  

 if(m==0) r=n+1; 

 else if(n==0) r=akm(m-1,1);  

 else { 

 g=akm(m,n-1);r=akm(m-1,g);//两次连着递归  }  

 return r;  }

 //（2）利用栈

 void main()

  { 

   int m=3;int n=2; 

   struct {

   int mval;

   int nval;

   int ack;}s[100]; 

   int top=0;

 s[top]mval=m;

 s[top]nval=n;

 s[top]ack=-1;

 while(s[0]ack==-1)

  { 

    if(s[top]mval==0)

     { s[top]ack=s[top]nval+1; 

       while(s[top]ack!=-1&&top)

       {

        top--;

        if(s[top]nval==-1){ s[top]nval=s[top+1]ack;} 

        else { s[top]ack=s[top+1]ack;} 

        } 

         } 

     else if(s[top]nval==0) 

            { 

            top++;

            s[top]mval=s[top-1]mval-1; 

            s[top]nval=1;

            s[top]ack=-1;

                  }

            else 

                 {

                  top++;

                  s[top]mval=s[top-1]mval-1; 

                  s[top]nval=-1; 

                  s[top]ack=-1;

                  top++;

                  s[top]mval=s[top-2]mval;

                  s[top]nval=s[top-2]nval-1;

                  s[top]ack=-1;

                  }

                     } 

 cout<<s[0]ack<<endl;}

并查集的“路径压缩”算法：在集合的查找过程中顺便将树的深度降低。采用路径压缩后，每一次查询所用的时间复杂度为增长极为缓慢的ackerman函数的反函数——α（x）。对于可以想象到的n，α（n）都是在5之内的。

两个问题：

1、Integer太小了，数据早就爆了；

2、栈的调用过头了，“exitcode = 201”的意思就是栈溢出。

事实上，阿克曼函数的值是极大的。

Ackermann(0,n)=n+1

Ackermann(1,n)=n+2

Ackermann(2,n)=2n+3

Ackermann(3,n)=2^(n+3)-3

Ackermann(4,n)=2^2^2^……^2-3，乘幂中共有n+3个2。

当m≥4，Ackermann函数的增长快得惊人。Ackermann(4,0)=13，Ackermann(4,1)=65533，Ackermann(4,2)=2^65536-3有19729位，而Ackermann(4,3)则即使是位数也不易估计。Ackermann(5,0)=65533，Ackermann(5,1)=Ackermann(4,65533)……

针对于小数据，你的程序没问题。

直接在ADAMS/CAR里建模，建完模里边有软件自带的几种仿真，比如双轮同向，反向激振，转向仿真，整车仿真等，运行完进入postprosessor界面，里面有很多软件自带的函数测量，选择要绘图的参数绘图就能绘制仿真过程中各个参数的变化，里面有ackerman这一项的，ADAMS/CAR很好用的，汽车建模比VIEW真实多了，就是需要添加一些通讯器，安装件，这些添加不好仿真就容易不成功

人类与低级动物的最大差别之一是人类具有思维能力，即对事物的理性反映。在实践的基础上，人们对客观世界产生了认识。人类的认识总有一个从低级的感性认识到高级的理性认识的发展过程。在感性认识阶段， 人们只能把握事物的片面的、现象的、外部的性质，感性认识的多次重复后， 人脑对事物的认识就有了飞跃， 产生了概念，进而作出判断，并在此基础上进行推理，逐步形成了关于事物的（自然）科学理论。

（自然）科学理论研究的是客观世界的规律，而科学理论的形成依赖于人的思维。那么，思维有没有规律？思维是人类的精神现象，不是研究物质的自然科学的研究对象。人们对于思维规律的研究就产生了思维科学。从某种意义上说，它包括心理学、哲学（之一部分）……

思维的基本特征是概括性与间接性，也就是说，思维反应现实是从特殊到一般、由表及里、由此及彼的。因此，这就要求人类具有形成概念、作出判断、进行推理的能力。（如若不然，人们就只能个别地、直接地认识客观事物。）逻辑学是研究人类推理的规律的学科，因而可以看作思维科学的一个分支。

所谓推理，就是从一个或几个已知判断推导出一个新的判断的思维过程。任何推理都有它形式和内容的两个方面。推理的内容是它所施用的具体的科学理论的研究对象，而逻辑学研究的是推理的形式， 也就是去除内容后前提判断与结论的关系。

发展历史

由上面的论述可见，逻辑学是一切科学的推理工具，是一种基础的学科。正因为逻辑学是如此重要， 人类对于逻辑学的研究很早就开始了。

逻辑学的创始人是马其顿（希腊）伟大的哲学家 Aristotle (前384-前322)，他的逻辑学著作是其继承者总称为《工具论》的6篇论文——《范畴篇》、《解释篇》、《分析前篇》、《分析后篇》、《辩论常识篇》、《辩谬篇》，其中研究了概念、判断、三段论推理、证明与反驳的方法等重要课题。实际上，他发现了演绎逻辑的一系列基本定律。

演绎推理的前提与结论之间有必然的联系，也就是说前提蕴涵结论。因此，在演绎逻辑中，只要前提真，结论必然真。但是，从思维的方面来看，演绎推理是从一般到特殊的，其结论没有超出前提所断定的范围。

新知识的发现有赖于另一种推理模式——归纳推理，它是由个别过渡到一般的推理。归纳推理的前提是一些关于个别事物的判断，结论都是关于这类事物的普遍性判断， 因而超出了前提的范围。值得注意的是， 归纳推理的结论不具有必然性。1620年英国哲学家 Bacon (1561-1626) 出版了《新工具论》，系统地论述了归纳方法， 奠定了归纳逻辑的基础。

思维是人类的精神现象，它的存在需要一个物质载体——语言。粗略地说，语言是思维的表达形式，而思维是语言表达的内容。推理是思维的一种形式，因而它也需要用语言加以表述。在逻辑学发展的早期，表达推理的语言都是自然语言。但是，自然语言具有多义、含混等特征， 这就经常会影响到推理的准确性。为了解决这个问题，德国数学家、哲学家 Leibniz (1649-1716) 提出了数理逻辑的基本思想：寻找一种通用的、精确的符号语言，以此基础建立一种逻辑演算，以便能用计算来解决争辩。 所以， Leibniz 被认为是数理逻辑的创始人。

在实现数理逻辑思想的进程中，首先应该提到的是英国数学家 Boole (1815-1864) 它应用代数方法研究逻辑学，于1847年出版了《逻辑的数学分析: 演绎推理的演算》，建立了命题代数。

1879年德国数学家 Frege (1848-1925) 出版了《概念文字》，引入了量词约束变元的概念，建立了谓词演算。

1910-1913年，英国哲学家、逻辑学家 Russell (1872-1970) 与 Whitehead (1860-1947) 出版了长篇巨著《数学原理》，给出了命题演算与谓词演算的完整的系统，但是它们的完备性仍然没有获得。

1918年德国数学家 Bernays (1888-1977) 在他的执教资格论文中表述并证明了命题演算的完备性。

1928年德国数学家 Hilbert (1862-1943) 与 Ackerman (1896-1962) 出版《数理逻辑基础》，将谓词演算的完备性作为悬而未决的问题表述出来。

1929年奥地利数学家 Gödel (1906-1978) 在他的博士论文中证明了谓词演算的完备性定理。至此，逻辑演算的体系最终完成，Leibniz 关于数理逻辑的思想得以实现。

研究内容

现代意义上的数理逻辑中的“数理”一词有两层意思：

其一是 Leibniz 的思想——用数学的方法研究逻辑；

其二是主要研究数学中使用的逻辑。

后者的源流是 20 世纪初人们对于数学基础的关注。

19 世纪末引入的集合的概念逐渐成为数学中最基本、最有用的概念之一，但它却引起了许多悖论（如 Russell 悖论， 最大序数、最大基数悖论）。为了排除悖论，人们发展了公理集合论。 另一方面，非 Euclidean 几何的出现刺激了人们去研究几何基础。1899 年 Hilbert 在几何基础的研究工作中发展了公理化方法。这样的一些事件汇合在一起，促使数学家们更进一步地对数学中概念的构成法与论证方法进行思考，从而在20世纪初产生了一个新的数学领域——数学基础。

数学基础所关心的问题与具体的数学分支中所研究的问题完全不同，是一些数学的元理论性质的问题，比如：“数学是什么？”“如何给数学奠定严格的理论基础？”

由于对这些问题的不同看法，出现了数学基础的不同流派，最主要的是:

Russell 的逻辑主义

Russell 认为数学是逻辑学的一个分支，并说“逻辑学是数学的青年时代，而数学是逻辑学的壮年时代”。特别地，它在与 Whitehead 合作的长篇巨著《数学原理》中从逻辑学的基本法则出发建立了自然数理论、实数理论以及解析几何学等。但是，在从逻辑学重建数学的过程中它不得不假设一些非逻辑的公理，如无穷公理。

Brouwer 的直觉主义

它与传统数学的主要区别是拒绝承认排中律（“A或非A”），从而使得数学中的一些强有力的方法（如反证法）无法使用。例如，通过证明“若没有 x 满足 A(x) 将导致矛盾”来断定“存在 x 使 A(x) 成立”，因为这种证明方法并不能实际给出给出满足 A(x) 的 x ，直觉主义学派不予承认。正因为这样，许多重要的数学理论无法在直觉主义逻辑中建立。

Hilbert 的形式主义

Hillbert 希望将数学彻底形式化，进而证明其相容性、完备性、可判定性；这就是所谓的 Hilbert 纲领。1931年 Gödel 证明了如下的不完备性定理：

如果对自然数理论（算术）形式化而获得的系统是相容的，则该系统必包含一逻辑公式 A，使得 A 与非 A 在系统中都不能证明；

设 S 为包含自然数理论的形式化系统，如果 S 是相容的，则只利用 S 中可形式化的论证不可能证明 S 的相容性。

这说明了对数学理论的形式化方法存在本质的限制，Hilbert 纲领是不能实现的。

虽然上述三大流派都没能彻底解决数学基础的问题，但它们的研究工作极大地丰富了数理逻辑这个学科，逐渐形成了下述四大领域:

公理集合论；

模型论；

递归函数论（可计算性理论）；

证明论（元数学）。