x^ n展开式是什么？

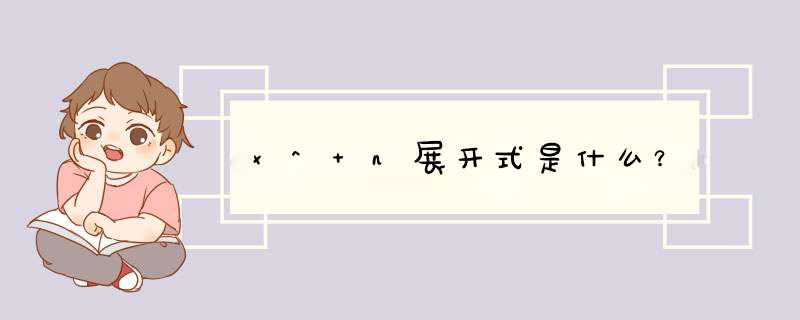
1+x的n次方展开式公式是：

（x-1)^n

=Cn0x^n+Cn1x^（n-1）（-1）^1+Cn2x^（n-2）（-1）^2+Cn（n-1）x（-1）^（n-1）+Cnn（-1）^n（x+1）^n

泰勒公式

泰勒公式是数学分析中重要的内容，也是研究函数极限和估计误差等方面不可或缺的数学工具，泰勒公式集中体现了微积分“逼近法”的精髓，在近似计算上有独特的优势。

利用泰勒公式可以将非线性问题化为线性问题，且具有很高的精确度，因此其在微积分的各个方面都有重要的应用。

泰勒公式可以应用于求极限、判断函数极值、求高阶导数在某点的数值、判断广义积分收敛性、近似计算、不等式证明等方面。

点(n,sn)均在函数y=2的x次方+r的图像上

sn=2^n+r

s(n-1)=2^(n-1)+r

两式相减得

sn-s(n-1)=an

=2^n-2^(n-1)

=22^(n-1)-2^(n-1)

=2^(n-1)

x的n次方是幂函数。x为底数n是指数，一般地形如y等于x^a其中a为常数的函数，即以底数为自变量幂为因变量，指数为常量的函数称为幂函数，C语言pow函数用来求x的y次方的值，当N等于0等于1，当N小于0等于X的n绝对值方分之1。

x的n次方特点

一个函数在某一点的导数描述了这个函数在这一点附近的变化率，如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率，不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。

若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导，然而可导的函数一定连续，不连续的函数一定不可导，求幂级数的和函数的方法，通常是或者先定积分后求导，或先求导后定积分，或求导定积分多次联合并用。

nx的n次方的和函数：{nx^(n-1)}=1/(1-x)^2。函数（function）的定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。

函数的近代定义是给定一个数集A，假设其中的元素为x，对A中的元素x施加对应法则f，记作f（x），得到另一数集B，假设B中的元素为y，则y与x之间的等量关系可以用y=f（x）表示，函数概念含有三个要素：定义域A、值域B和对应法则f。其中核心是对应法则f，它是函数关系的本质特征。

#include<stdioh>

double power(double x, int n)

{

        double p=10;

        while(n>0) {

                p=px;

                n--;

        }

        return p;

}

int main(void)

{

        double x;

        int n;

        scanf("%lf %d",&x,&n);

        printf("%lf\n",power(x,n));

        return 0;

}