关于MATLAB 卷积积分的实现

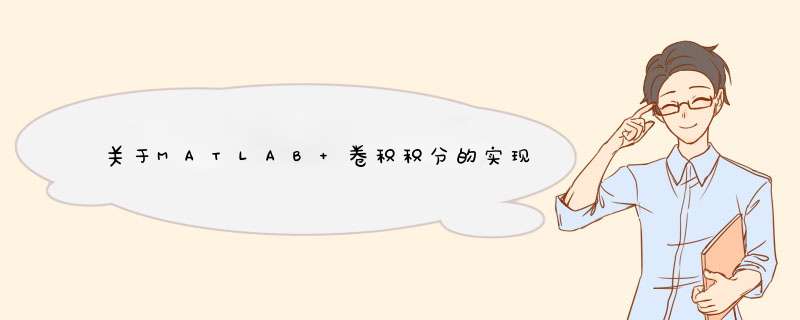
p=001;

t1=0:p:1;

f1=ones(size(t1));

t2=1:p:3;

f2=ones(size(t2));

f=conv(f1,f2);        %计算序列x与h的卷积和f

f=fp;

t0=t1(1)+t2(1);        %计算序列f非零样值的起点位置

t3=length(f1)+length(f2)-2;     %计算卷积和f的非零样值的宽度

t=t0:p:(t3p+t0);                       %确定卷积和f非零样值的时间向量

subplot(2,2,1)

plot(t1,f1)         %在子图1绘x(t)时域波形图

title('x(t)')

xlabel('t1')

ylabel('x(t)')

subplot(2,2,2)

plot(t2,f2)          %在子图2绘h(t)时波形图

title('h(t)')

xlabel('t2')

ylabel('h(t)')

subplot(2,2,3)

plot(t,f);          %画卷积y(t)的时域波形

h=get(gca,'position');                     %获取坐标轴的未知属性

h(3)=25h(3);

set(gca,'position',h)    %将第三个子图的横坐标范围扩为原来的25倍

title('y(t)=x(t)h(t)')

xlabel('t')

ylabel('y(t)')

如果你要的是符号卷积那就没有直接的功能函数要自己写出卷积表达式，再用符号积分函数去积，经常积不出如果是数值积分（序列）有conv这一族函数（help里面有相关函数那些）其实你要卷积还不如直接去算F变换再去求反变换来的方便

== TA α n=0:50; %定义序列的长度是 50 A=1; %设置信号有关的参数 a=04; T=1; %采样率 w0=20734; x=Aexp(-anT)sin(w0nT); %pi 是 MATLAB 定义的π，信号乘可采用“ ” close all %清除已经绘制的 x(n)图形 subplot(3,1,1);stem(x); %绘制 x(n)的图形 title(‘理想采样信号序列 ’); k=-25:25; W=(pi/125)k; X=x(exp(-jpi/125))^(n’k); magX=abs(X); %绘制 x(n)的幅度谱 subplot(3,1,2);stem(magX);title(‘理想采样信号序列的幅度谱 ’); angX=angle(X); %绘制 x(n)的相位谱 subplot(3,1,3);stem(angX) ; title (‘理想采样信号序列的相位谱 ’) 2、单位脉冲序列 在 MatLab 中，这一函数可以用 zeros 函数实现： n=1:50; %定义序列的长度是 50 x=zeros(1,50); %注意： MATLAB 中数组下标从 1 开始 x(1)=1; close all; subplot(3,1,1);stem(x);title(‘单位冲击信号序列 ’); k=-25:25; X=x(exp(-jpi/125))^(n’k); magX=abs(X); %绘制 x(n)的幅度谱 subplot(3,1,2);stem(magX);title(‘单位冲击信号的幅度谱 ’); angX=angle(X); %绘制 x(n)的相位谱 subplot(3,1,3);stem(angX) ; title (‘单位冲击信号的相位谱 ’) 3、矩形序列 n=1:50 x=sign(sign(10-n)+1); close all; subplot(3,1,1);stem(x);title(‘单位冲击信号序列 ’); k=-25:25; X=x(exp(-jpi/25))^(n’k); magX=abs(X); %绘制 x(n)的幅度谱 subplot(3,1,2);stem(magX);title(‘单位冲击信号的幅度谱 ’); angX=angle(X); %绘制 x(n)的相位谱 subplot(3,1,3);stem(angX) ; title (‘单位冲击信号的相位谱 ’) 4、特定冲击串： )3()2(52)1(52)()( +++= nnnnnx δδδδ n=1:50; %定义序列的长度是 50 x=zeros(1,50); %注意： MATLAB 中数组下标从 1 开始 x(1)=1;x(2)=25;x(3)=25;x(4)=1; close all; subplot(3,1,1);stem(x);title(‘单位冲击信号序列 ’); k=-25:25; X=x(exp(-jpi/125))^(n’k); magX=abs(X); %绘制 x(n)的幅度谱 subplot(3,1,2);stem(magX);title(‘单位冲击信号的幅度谱 ’); angX=angle(X); %绘制 x(n)的相位谱 subplot(3,1,3);stem(angX) ; title (‘单位冲击信号的相位谱 ’) 5、卷积计算： ∑ +∞ ∞= == m mnhmxnhnxny )()()()()( 在 MATLAB 中。提供了卷积函数 conv，即 y=conv(x,h)，调用十分方便。例如： 系统： )3()2(52)1(52)()( +++= nnnnnh b δδδδ 信号： 500),sin()( 0 <≤= nnTAetx nT a α n=1:50; %定义序列的长度是 50 hb=zeros(1,50); %注意： MATLAB 中数组下标从 1 开始 hb(1)=1;hb(2)=25;hb(3)=25;hb(4)=1; close all; subplot(3,1,1);stem(hb);title(‘系统 hb[n]’); m=1:50; %定义序列的长度是 50 A=444128; %设置信号有关的参数 a=50sqrt(20)pi; T=0001; %采样率 w0=50sqrt(20)pi; x=Aexp(-amT)sin(w0mT); %pi 是 MATLAB 定义的π，信号乘可采用“ ” subplot(3,1,2);stem(x);title(‘输入信号 x[n]’); y=conv(x,hb); subplot(3,1,3);stem(y);title(‘输出信号 y[n]’); 6、卷积定律验证 k=-25:25; X=x(exp(-jpi/125))^(n’k); magX=abs(X); %绘制 x(n)的幅度谱 subplot(3,2,1);stem(magX);title(‘输入信号的幅度谱 ’); angX=angle(X); %绘制 x(n)的相位谱 subplot(3,2,2);stem(angX) ; title (‘输入信号的相位谱 ’) Hb=hb(exp(-jpi/125))^(n’k); magHb=abs(Hb); %绘制 hb(n)的幅度谱 subplot(3,2,3);stem(magHb);title(‘系统响应的幅度谱 ’); angHb=angle(Hb); %绘制 hb(n)的相位谱 subplot(3,2,4);stem(angHb) ; title (‘系统响应的相位谱 ’) n=1:99; k=1:99; Y=y(exp(-jpi/125))^(n’k); magY=abs(Y); %绘制 y(n)的幅度谱 subplot(3,2,5);stem(magY);title(‘输出信号的幅度谱 ’); angY=angle(Y); %绘制 y(n)的相位谱 subplot(3,2,6);stem(angY) ; title (‘输出信号的相位谱 ’) %以下将验证的结果显示 XHb=XHb; Subplot(2,1,1);stem(abs(XHb));title(‘x(n)的幅度谱与 hb(n)幅度谱相乘 ’); Subplot(2,1,2);stem(abs(Y);title(‘y(n)的幅度谱 ’); axis([0,60,0,8000])

在MATLAB中，可以用函数y=filter(p,d,x)实现差分方程的仿真，也可以用函数y=conv(x,h)计算卷积。

（1）即y=filter(p,d,x)用来实现差分方程，d表示差分方程输出y的系数，p表示输入x的系数，而x表示输入序列。输出结果长度数等于x的长度。

实现差分方程，先从简单的说起：

filter([1,2],1,[1,2,3,4,5])，实现y[k]=x[k]+2x[k-1]

y[1]=x[1]+20=1    (x[1]之前状态都用0)

y[2]=x[2]+2x[1]=2+21=4

（2）y=conv(x,h)是用来实现卷级的，对x序列和h序列进行卷积，输出的结果个数等于x的长度与h的长度之和减去1。

卷积公式：z(n)=x(n)y(n)= ∫x(m)y(n-m)dm

程序一：以下两个程序的结果一样

（1）h = [3 2 1 -2 1 0 -4 0 3]; % impulse response

          x = [1 -2 3 -4 3 2 1]; % input sequence

         y = conv(h,x);

         n = 0:14;

         subplot(2,1,1);

         stem(n,y);

         xlabel('Time index n'); ylabel('Amplitude');

        title('Output Obtained by Convolution'); grid;

（2）x1 = [x zeros(1,8)];

          y1 = filter(h,1,x1);

          subplot(2,1,2);

         stem(n,y1);

         xlabel('Time index n'); ylabel('Amplitude');

         title('Output Generated by Filtering'); grid;

比如两个信号f1=sin(t)/t和f2=sin(t)，我想得到两个函数的卷积式不是不可能不是矩阵

matlab中所有数据都是矩阵表示不信你试试

a=1

size(a)