origin中如何进行曲线拟合 *** 作？

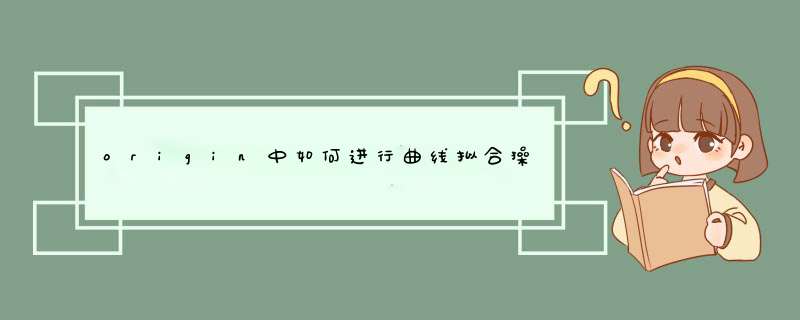
1、首先打开Origin ,输入待处理的数据，并绘制出数据的散点图。

2、打开annlysis -> Fitting -> Nonlinear Curve Fit -> Opea Dialog 非线性曲线拟合函数对话框。

3、点击，制作并编辑函数。

4、新建自定义函数文件夹和函数。当然也可以把自定义的函数放入 Origin 内置的函数文件夹中。

5、编辑所需要的函数。图中有一些对特定项的描述。

6、这时生成函数。

7、返回到拟合函数列表，找到自己自定义的函数，开始进行拟合，如下图所示就完成了。

首先，数据拟合是需要根据你的实验符合的数学模型进行拟合，你需要了解你的数据符合哪种函数，然后根据这个函数对你采集到的实验数据进行拟合。 至于具体的拟合步骤，需要在 Analysis — Non-linear Curve Fit — Advanced Fitting Tool 在d出的对话框左侧是多项式的项数，有线性Line Mode，多项式Poly，常数 Constent，线性line，Parabalo抛物线，Cubic三次方，Poly4，Poly5 等，右侧的白框中会显示相应的函数表达式。 如果这里没有你需要的多项式，可以点击对话框右下侧的 More，选择更多的函数类型。在新对话框中，左上Categories中有各种常用的函数类型，右上方Functions 里有相应的具体函数形式，下方的方框中有其函数表达式Equation，曲线形式Sample Curve，和函数文件Function File（这个可以不用管，除非你想编程）选择符合你实验的函数，然后调整各个参数值进行拟合工作。 然后点击上方的工具栏中 Action — Fit，点击 100 Iter ，Done

origin中将几条应力应变曲线拟合成一条曲线的方法如下：

（1）确保5条曲线的起始点一致；

（2）将5组数据在worksheet里依次连在一起；

（3）拟合。

若其中有试样的初始应力应变曲线段不真实（如加载系统有间隙等），则不应做“综合拟合”处理。

Origin为OriginLab公司出品的较流行的专业函数绘图软件，是公认的简单易学、 *** 作灵活、功能强大的软件，既可以满足一般用户的制图需要，也可以满足高级用户数据分析、函数拟合的需要。Origin自1991年问世以来，由于其 *** 作简便，功能开放，很快就成为国际流行的分析软件之一，是公认的快速、灵活、易学的工程制图软件。

1、首先使用红外线软件omnic打开红外线文件（通常为SPA格式），单击“文件”-“另存为”-文件格式为CSV格式。

2、使用Excel打开保存的CSV文件，复制两列数据，打开原始软件，将数据复制到工作表中，然后绘制一条曲线。

3、然后单击“分析”-“拟合”-“拟合多峰”。

4、d出对话框如下。 在“峰数”中输入所需的峰数，然后单击“确定”。

5、出现另一个对话框，然后单击“确定”。 按照提示双击峰的中心，选择后单击“确定”，将显示拟合的曲线。

6、如果仅需要曲线的数据，则可以在工作簿中找到它，如下所示：

7、选择两列数据A1（X）和Peaksum，使曲线成为峰。

1、在origin里面，通过图示位置来选择函数图标。

2、这个时候进入新的窗口，直接确定需要的对象。

3、下一步等完成上述 *** 作以后，如果没问题就点击OK按钮。

4、这样一来会得到相关的效果图，即可拟合二次函数图像了。

1、首先打开SPSS软件后先打开你需要分析的数据，打开右上角的标识，选择你需要的文件，点击打开，选择文件。

2、其次打开后如果你事先不知道两个变量之间是线性还是非线性，那就画散点图分析其趋势。

3、最后确定不是线性关系之后，用曲线拟合分析。

用Excel，输入数据后，选定数据，然后点击“插入”，找到“散点图”，画出散点图，选中散点图的曲线（没趋势线的就选择点），右键，“添加趋势线”或“设置趋势线格式”，可以看见有不同的拟合可以选择。选中某个后，可以勾选“显示公式”以及“显示R的平方”，可以查看公式以及拟合程度。

1、打开origin80的相关表格，输入log函数的基本数据。

2、下一步，需要选择在X、Y轴上进行拟合的数据。

3、这个时候，可以点击表格下方图形类型的对应按钮。

4、这样一来通过得到相应的图形结果以后，即可用origin80进行log函数拟合了。