xn的和函数

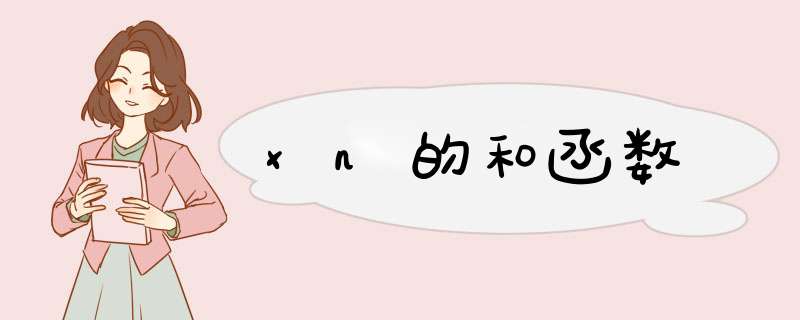
∑(i从1到n)x^i=x(1-x^n)/(1-x)

x的绝对值小于1且当n趋于无穷的时候,

∑(n→∞)x^n=x/(1-x)

上面说的是x的幂从1开始的

但如果幂从0开始的话就是

∑(n从0到∞)x^n=1/(1-x)

关键是幂从0开始还是从1开始

对于你这个原题n肯定是从1开始的,因为有一个(n-1)

(x^n/n)'=x^(n-1)

利用导数去除变量系数

=(1/x)∫∑x^(n-1)/2^ndx

根据和函数下限算出和函数然后算积分

函数的近代定义

是给定一个数集A，假设其中的元素为x，对A中的元素x施加对应法则f，记作f（x），得到另一数集B，假设B中的元素为y，则y与x之间的等量关系可以用y=f（x）表示，函数概念含有三个要素：定义域A、值域B和对应法则f。其中核心是对应法则f，它是函数关系的本质特征。

考虑级数收敛的条件，根据比值判别法，当 |x| < 1 时，级数绝对收敛，因此在这个收敛域内，可以对级数进行求和。

设 S(x) 为级数的和函数，即：

S(x) = ∞∑n=1 1/n x^(n-1)

对 S(x) 进行求导，得到：

S'(x) = ∞∑n=1 d/dx (1/n x^(n-1))

对其中的每一项进行求导，得到：

d/dx (1/n x^(n-1)) = 1/n d/dx (x^(n-1)) = x^(n-2)

因此，有

S'(x) = ∞∑n=1 x^(n-2)

对求和式进行变形，得到：

S'(x) = x^(-1) + x^0 + x^1 + x^2 +

这是一个等比数列，公比为 x，因此可以求得：

S'(x) = x^(-1) / (1-x)

对 S'(x) 进行不定积分，得到：

S(x) = ln|x| - ln|1-x| + C

其中 C 为常数。因为 S(0) = 0，所以 C = 0，因此有：

S(x) = ln|x| - ln|1-x|

因此，对于 |x| < 1，级数的和函数为 S(x) = ln|x| - ln|1-x|。

解：

令S=x+2x^2++nx^n

xS=x^2+2x^3++nx^(n+1)

若x≠1则

相减得

(1-x)S=x+x^2++x^n-nx^(n+1)

=[x^(n+1)-x]/(x-1)-nx^(n+1)

几何含义

函数与不等式和方程存在联系（初等函数）。令函数值等于零，从几何角度看，对应的自变量的值就是图像与X轴的交点的横坐标；从代数角度看，对应的自变量是方程的解。另外，把函数的表达式（无表达式的函数除外）中的“=”换成“<”或“>”，再把“Y”换成其它代数式，函数就变成了不等式，可以求自变量的范围。

S(x)=∑(0~无穷)nx^(n-1)

∫ S(x) dx= ∫ ∑(0~无穷)nx^(n-1) dx

=∑(0~无穷) ∫ nx^(n-1) dx

=∑(0~无穷) x^n 等比求和

=1/(1-x)

S(x)=(1/(1-x))'=1/(1-x)^2