MATLAB仿真

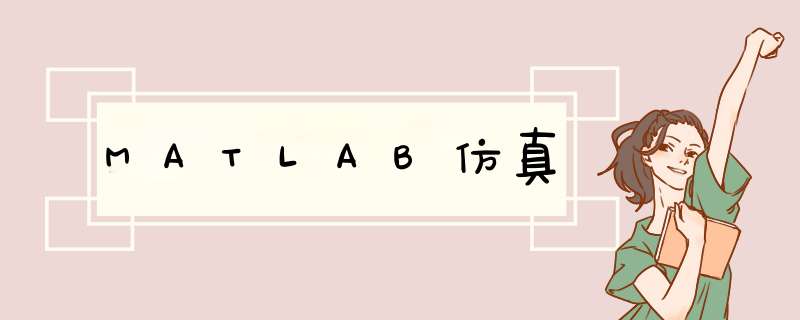
num=[2]； %传递函数分子系数向量

den=[1 4 7 08]； %传递函数分母系数向量

figure(1)； %创建图形窗口1

rlocus(num,den)； %绘制根轨迹图

figure(2)； %创建图形窗口2

nyquist(num,den)； %绘制频率特性图

先介绍一下simulink的仿真过程（以便理解s函数），simulink的仿真有两个阶段： 一个为初始化，这个阶段主要是设置一些参数，像系统的输入输出个数、状态初值、 采样时间等；第二个阶段就是运行阶段，这个阶段里要进行计算输出、更新离散状态、 计算连续状态等等，这个阶段需要反复运行，直至结束。

在matlab的workspace里打edit sfuntmpl(这是matlab自己提供的s函数模板)，我们 看它来具体分析s函数的结构。 它的第一行是这样的：function [sys,x0,str,ts]=sfuntmpl(t,x,u,flag)

先讲输入与输出变量的含义：t是采样时间，x是状态变量，u是输入（是做成simulink模 块的输入）,flag是仿真过程中的状态标志（以它来判断当前是初始化还是运行等）；sys输出根据flag的不同而不同（下面将结合flag来讲sys的含义），x0是状态变量的初始值，str是保留参数（mathworks公司还没想好该怎么用它，嘻嘻，一般在初始化中将它置空就可以了,str=[])，ts是一个1×2的向量，ts(1)是采样周期，ts(2)是偏移量。

下面结合sfuntmplm中的代码来讲具体的结构：

switch flag, %判断flag，看当前处于哪个状态

case 0,

[sys,x0,str,ts]=mdlInitializeSizes;

flag=0表示处于初始化状态，此时用函数mdlInitializeSizes进行初始化，此函数在 sfuntmplm的149行

我们找到他，在初始化状态下，sys是一个结构体，用它来设置模块的一些参数，各个参 数详细说明如下

size = simsizes;%用于设置模块参数的结构体用simsizes来生成

sizesNumContStates = 0;%模块连续状态变量的个数

sizesNumDiscStates = 0;%模块离散状态变量的个数

sizesNumOutputs = 0;%模块输出变量的个数

sizesNumInputs = 0;%模块输入变量的个数

sizesDirFeedthrough = 1;%模块是否存在直接贯通（直接贯通我的理解是输入能 %直接控制输出）

sizesNumSampleTimes = 1;%模块的采样时间个数，至少是一个

sys = simsizes(sizes); %设置完后赋给sys输出

举个例子，考虑如下模型：

dx/dt=fc(t,x,u) 也可以用连续状态方程描述：dx/dt=Ax+Bu

x(k+1)=fd(t,x,u) 也可以用离散状态方程描述：x(k+1)=Hx(k)+Gu(k)

y=fo(t,x,u) 也可以用输出状态方程描述：y=Cx+Du

设上述模型连续状态变量、离散状态变量、输入变量、输出变量均为1个，我们就只需改上面那一段代码为：

（一般连续状态与离散状态不会一块用，我这儿是为了方便说明）

sizesNumContStates=1;sizesNumDiscStates=1;sizesNumOutputs=1;sizesNumInpu

ts=1;

其他的可以不变。继续在mdlInitializeSizes函数中往下看：

x0 = []; %状态变量设置为空，表示没有状态变量，以我们上面的假设，可改 %为x0=[0,0](离散和连续的状态变量我们都设它初值为0)

str = []; %这个就不用说了，保留参数嘛，置[]就可以了，反正没什么用，可 %能70会给它一些意义

ts = [0 0]; %采样周期设为0表示是连续系统，如果是离散系统在下面的mdlGet %TimeOfNextVarHit函数中具体介绍

嘻嘻，总算讲完了初始化，后面的应该快了

在sfuntmpl的106行继续往下看：

case 1,

sys=mdlDerivatives(t,x,u);

flag=1表示此时要计算连续状态的微分，即上面提到的dx/dt=fc(t,x,u)中的dx/dt,找到 mdlDerivatives函数（在193行）如果设置连续状态变量个数为0，此处只需sys=[]; 就可以了（如sfuntmpl中一样），按我们上述讨论的那个模型，此处改成 sys=fc(t,x(1),u)或sys=Ax(1)+Bu %我们这儿x(1)是连续状态变量，而x(2)是离散的 ，这儿只用到连续的，此时的输出sys就是微分

继续，在sfuntmpl的112行：

case 2,

sys=mdlUpdate(t,x,u);

flag=2表示此时要计算下一个离散状态，即上面提到的x(k+1)=fd(t,x,u)，找到mdlUpd ate函数（在206行）它这儿sys=[];表示没有离散状态，我们这而可以改成 sys=fd(t,x(2),u)或sys=Hx(2)+Gu;%sys即为x(k+1)

看来后面几个一两句话就可了，呵呵，在sfuntmpl的118行

case 3,

sys=mdlOutputs(t,x,u);

flag=3表示此时要计算输出，即y=fo(t,x,u),找到mdlOutputs函数（在218行），如上，如果sys=[]表示没有输出，我们改成sys=fo(t,x,u)或sys=Cx+Du %sys此时为输出y

好像快完了，嘻嘻，在sfuntmpl的124行

case 4,

sys=mdlGetTimeOfNextVarHit(t,x,u);

flag=4表示此时要计算下一次采样的时间，只在离散采样系统中有用(即上文的mdlInit ializeSizes中提到的ts设置ts(1)不为0)

连续系统中只需在mdlGetTimeOfNextVarHit函数中写上sys=[];这个函数主要用于变步长的设置，具体实现大家可以用edit vsfunc看vsfuncm这个例子

最后一个，在sfuntmpl的130行

case 9,

sys=mdlTerminate(t,x,u);

flag=9表示此时系统要结束，一般来说写上在mdlTerminate函数中写上sys=[]就可，如 果你在结束时还要设置什么，就在此函数中写

关于sfuntmpl这个s函数的模板讲完了。

s函数还可以带用户参数，下面给个例子，和simulink下的gain模块功能一样，大伙自己 看吧，我睡觉去了，累了

function [sys,x0,str,ts] = sfungain(t,x,u,flag,gain)

switch flag,

case 0,

sizes = simsizes;

sizesNumContStates = 0;

sizesNumDiscStates = 0;

sizesNumOutputs = 1;

sizesNumInputs = 1;

sizesDirFeedthrough = 1;

sizesNumSampleTimes = 1;

sys = simsizes(sizes);

x0=[];

str=[];

ts=[0,0];

case 3,

sys=gainu;

case {1,2,4,9},

sys = [];

end

做好了s函数后，simulink--user-defined function下拖一个S-Function到你的模型，就可以用了 在simulink----user-defined function还有个s-Function Builder，他可以生成用c语 言写的s函数 在matlab的workspace下打sfundemos，可以看到很多演示s函数的程序。

先打开simulink，新建模型文件，然后从模块库里拖出传递函数模块，双击，设置传递函数的表达式，你这种最好用零极点模型，然后在拖出来一个延迟模块，双击设置延迟时间tao。接着把这两个模块串联起来。然后拖出一个step信号源和一个比较点，把他们之间连起来，再接一个负反馈到比较点，就完成了(如果这个直接是闭环函数的话，比较点和负反馈就不要了)，样子就和框图一样。输出这里可以根据需要接一个simout或者示波器。然后设置仿真时间，点那个三角箭头开始仿真。

　　问题：这是一个函数，Not enough input arguments 的意思是输入的参数不够。这里的参数有 t,x,u,flag共四个，都需要你输入。

　　解决方法：

　　方式1：调试函数的时候直接 run运行 然后写入参数回车 即可(在命令窗口能看到结果)，如图1所示；（如果是新建的mat文件 需要需要以函数名命名 “spacemodelm”）

　                                          图1 函数直接调试

　　方式2：保存好函数之后，直接在命令窗口（如图2所示）或者在你的主程序里调用即可。

                                                    图2 命令窗口调试

　　希望对你有所帮助。。。

1、你在Simulink里的PID控制器应该是PID Controller做的吧？如果换PID Controller (with Approximate Derivative)应该会得到和用step函数类似的效果（和N的取值有关）。

2、一阶延迟模型只是用于过程控制系统PID控制器设计的近似模型，并非实际的模型。一般的做法是，用这个模型提炼出KTL三个参数，然后计算出控制器参数，接下来应该是把控制器用于对象原来的模型，而不是这个FOLPD模型。

3、至于为什么控制器使用纯微分和近似微分会有这么大的差别，以及为什么加入延迟之后会有这样的现象，这些深层的原因我没想明白，仅此提供一些自己知道的信息，供参考。