C++刷题之旅（42）

LeetCode算法入门（第四十二天） 树 108将有序数组转换为二叉搜索树

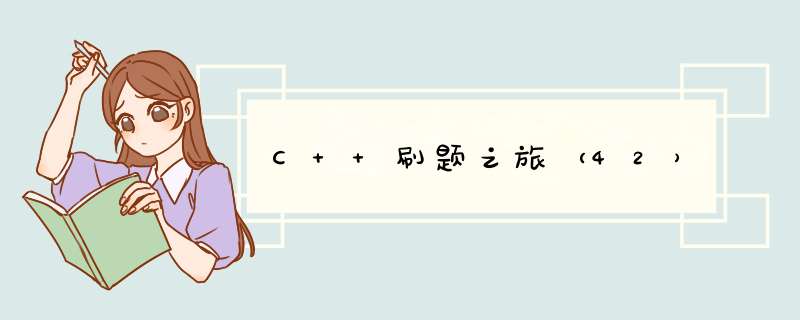
数组的元素已经升序排好，每次寻找数组中点，分为左右区间，即左右子节点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* traversal(vector<int> nums, int left, int right){
        if(left > right) 
            return nullptr;

        int mid = left + ((right - left) / 2);    //取中点
        TreeNode* root = new TreeNode(nums[mid]);  //创建节点
        root->left = traversal(nums, left, mid-1);  //更新左节点
        root->right = traversal(nums, mid+1, right);    //更新右节点
        return root;
    }

    TreeNode* sortedArrayToBST(vector<int>& nums) {
       TreeNode* root = traversal(nums, 0, nums.size()-1);
       return root;
    }
};

105.从前序与中序遍历序列构造二叉树

前序遍历形式：[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
中序遍历形式：[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
根节点总是前序遍历中的第一个节点，只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目，左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    unordered_map<int,int> pos;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for(int i = 0; i < n; i++)
            pos[inorder[i]] = i; //记录中序遍历的根节点位置
        return dfs(preorder,inorder,0,n-1,0,n-1);        
    }
    //pl,pr对应一棵子树的先序遍历区间的左右端点
    //il,ir对应一棵子树的中序遍历区间的左右端点
    TreeNode* dfs(vector<int>&pre,vector<int>&in,int pl,int pr,int il,int ir)
    {
        if(pl > pr || il > ir)  return NULL; //子树为空
        int k = pos[pre[pl]] - il; // pos[pre[pl]]是中序遍历中根节点位置，k是子树先序和中序遍历的长度
        TreeNode* root = new TreeNode(pre[pl]);
         // 先序遍历中「从 左边界+1 开始到左子树节点数目的元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
         // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root->left = dfs(pre,in,pl+1,pl+k,il,il+k-1);  //左子树前序遍历，左子树中序遍历
        root->right = dfs(pre,in,pl+k+1,pr,il+k+1,ir); //右子树前序遍历，右子树中序遍历
        return root;
    }
};

103.二叉树的锯齿形层序遍历

先从左到右，在从右到左，利用双端队列来控制当层节点值输出的顺序。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        if(!root) return ans;
        bool left_flag = true;    //是否从左往右遍历的标志
        queue<TreeNode> que;    
        que.push(*root);    
        while(!que.empty()){
            deque<int> dlist;   //定义一个双端队列储存当前层的值，方便调换方向， 局部变量
            int n = que.size();   //当前层节点的个数
            for(int i = 0; i < n; i++){
                auto node = que.front();   //取节点
                que.pop();
                if(left_flag){
                    dlist.push_back(node.val);   //存入顺序和读取下一层顺序一致
                }else{
                    dlist.push_front(node.val);  //反向存入，即反向遍历
                }
                //将下一层的节点入队
                if(node.left) que.push(*node.left);
                if(node.right) que.push(*node.right);
            }
            ans.push_back(vector<int>{dlist.begin(), dlist.end()});  //每遍历完一层，压入到ans中
            left_flag = !left_flag;   //遍历完一层，标志位转换
        }
        return ans;
    }
};