LeetCode【121题】—买股票的最佳时机

leetcode-买股票的最佳时机

---

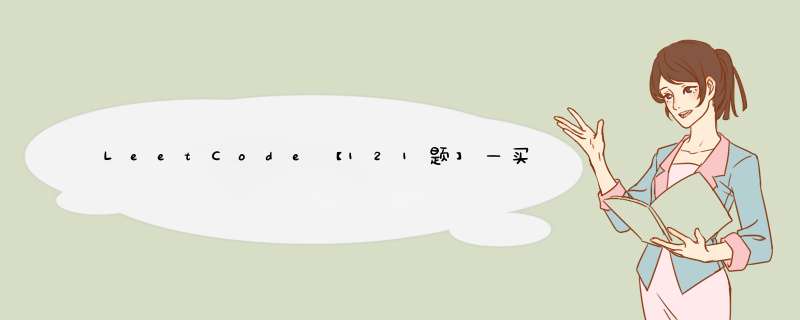
1.题目描述

---

2.暴力解法

基本思路： 对当天的股价，计算以后所有可能的利润，选取最大利润进行返回。

时间复杂度为O(n^2)，空间复杂度为O(1)。

 class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //暴力解法
        //时间复杂度为O(n^2)，空间复杂度为O(1)
        int maxProfit = 0;
        int Profit = 0;
        for(int i=0;i<prices.size();i++) {
            for(int j=i+1;j<prices.size();j++) {
                Profit = prices[j] - prices[i];
                if(Profit>maxProfit) {
                    maxProfit =Profit;
                }
            }
        }
        return maxProfit;
    }
};

---

3.动态规划算法

基本思路： (1)初始化最小价格为prices[0]，最大利润为0；(2)若当前价格大于最小价格，则计算利润。

否则，则最小价格等于当前价格；(3)判断是否为最大利润。

@@ 时间复杂度为O(n)，空间复杂度为O(1)。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //动态规划算法
        //此题类似于最大子数组和
        //时间复杂度为O(n),空间复杂度为O(1)
        int maxProfit = 0;
        int n =prices.size();
        int cur_price = prices[0];
        for(int i=1;i<n;++i) {
            if(prices[i]<=cur_price) {
                cur_price = prices[i];
            } else {
                Profit = prices[i]-cur_price;
            }
            if(Profit>maxProfit) {
                maxProfit = Profit;
            }
        }
        return maxProfit;
    }
};

---

4.动态规划算法代码优化

对于(3)中的代码， 我们可以使用C++中的auto关键字，max和min *** 作进行优化，提高代码的执行效率。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int maxProfit = 0 ,min_price = prices[0];
        for(auto& price:prices) {
            maxProfit = max(price-min_price,maxProfit);
            min_price = min(min_price,price);
        }
        return maxProfit;
    }
};