力扣 111 104二叉树的最大深度和最小深度总结

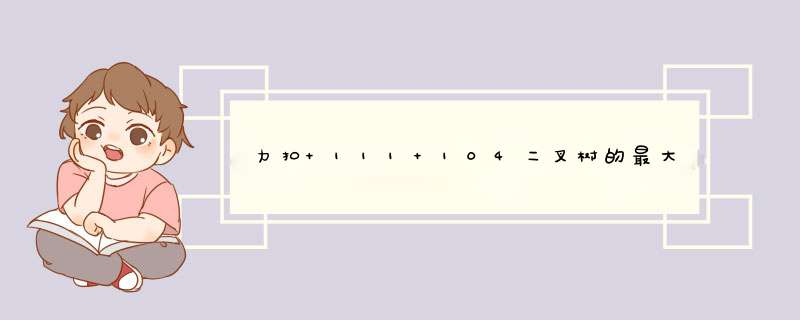
// 力扣104 二叉树最大深度

// 递归方法

class Solution {
public:
    int maxDepth(TreeNode* root) {
       if(!root)
       {
           return 0;
       }
       int left = maxDepth(root->left)+1;
       int right = maxDepth(root->right)+1;
       return left>right?left:right;
    }
};

//队列方法
class Solution {
public:
    int maxDepth(TreeNode* root) {
        int x = 0;
        queue<TreeNode*>qu;
        if(root!=nullptr)
        {
            qu.push(root);
        }
        while(!qu.empty())
        {
            int size = qu.size();
            for(int i=0;i<size;i++)
            {
                TreeNode* Node = qu.front();
                qu.pop();
                if(Node->left)qu.push(Node->left);
                if(Node->right)qu.push(Node->right);
                if(i == (size-1))
                {
                    x++;
                }
            }
        }
        return x;
    }
};

// 二叉树的最小深度
// 递归方法
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(!root)
        {
            return 0;
        }
        if(!root->left&&!root->right)//全是空节点
        {
            return 1;
        }
        else if(!root->left&&root->right||!root->right&&root->left)//空节点为左右节点中的两个当中的一个
        {
            root = root->left?root->left:root->right;
            return minDepth(root)+1;
        }
        else
        {
        int left = minDepth(root->left)+1;
        int right = minDepth(root->right)+1;
        return left>right?right:left;
        }
    }
};
// 队列方法

class Solution {
public:
    int minDepth(TreeNode* root) {
       queue<TreeNode*>qu;
       int count = 0;
       if(root!=nullptr)
       {
           qu.push(root);
           count = 1;
       }
       while(!qu.empty())
       {
           int size = qu.size();
           for(int i=0;i<size;i++)
           {
               TreeNode* Node = qu.front();
               qu.pop();
               if(Node->left)qu.push(Node->left);
               if(Node->right)qu.push(Node->right);
               if( !Node->left && !Node->right)//判断两个节点为空的时候，直接返回count
               {
                   return count;
               }
           }
           count++;
       }
       return count;
    }
};