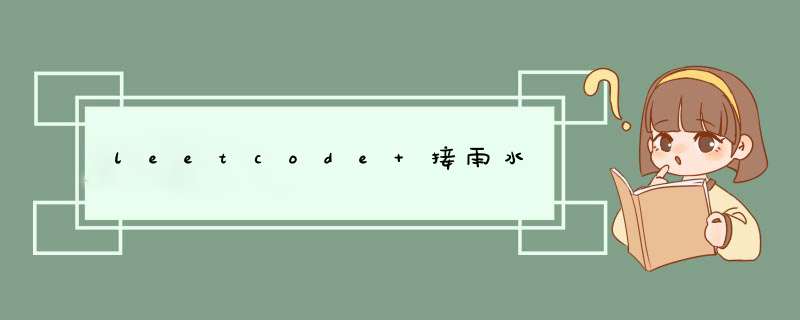
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
提示:
- n == height.length
- 1 <= n <= 2 * 104
- 0 <= height[i] <= 105
初次看到这个题目,要明确接雨水是如何计算的。也就是找出下雨后水能达到的最高位置,可以看出其等于两边最大高度的较小值减去当前高度的值。不难想到可以对于每一个位置,找到左右的最高点。
public int trap(int[] height) {
int ans = 0;
int size = height.length;
for (int i = 1; i < size - 1; i++) {
int max_left = 0, max_right = 0;
for (int j = i; j >= 0; j--) {
max_left = Math.max(max_left, height[j]);
}
for (int j = i; j < size; j++) {
max_right = Math.max(max_right, height[j]);
}
ans += Math.min(max_left, max_right) - height[i];
}
return ans;
}
可以看到其复杂度为O(N2);数组中的每个元素都需要向左向右扫描。
优化的思路就是我们能不能够一次遍历就可以确定呢?上述做法的时间复杂度较高是因为需要对每个下标位置都向两边扫描。如果已经知道每个位置两边的最大高度,则可以在 O(n)的时间内得到能接的雨水总量。 因此可以正向遍历数组 height 得到数组 leftMax 的每个元素值,反向遍历数组height 得到数组 rightMax 的每个元素值。 这里的时间复杂度为O(N),空间复杂度为O(N).,那么还能再降吗? 至此优化结束。 这个题还是很值得回味的,一步步,从原始的暴力,到动态规划,到最后的双指针,都是面试中的常考点。 欢迎分享,转载请注明来源:内存溢出
我们可以创建两个长度为 n 的数组 leftMax 和 rightMax。对于 0≤ipublic int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int[] leftMax = new int[n];
leftMax[0] = height[0];
for (int i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
int[] rightMax = new int[n];
rightMax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
}
注意到下标 i 处能接的雨水量由 leftMax[i] 和 rightMax[i] 中的最小值决定。由于数组 leftMax 是从左往右计算,数组 rightMax 是从右往左计算,因此可以使用双指针和两个变量代替两个数组。public int trap(int[] height) {
int ans = 0;
int left = 0, right = height.length - 1;
int leftMax = 0, rightMax = 0;
while (left < right) {
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
++left;
} else {
ans += rightMax - height[right];
--right;
}
}
return ans;
}

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)