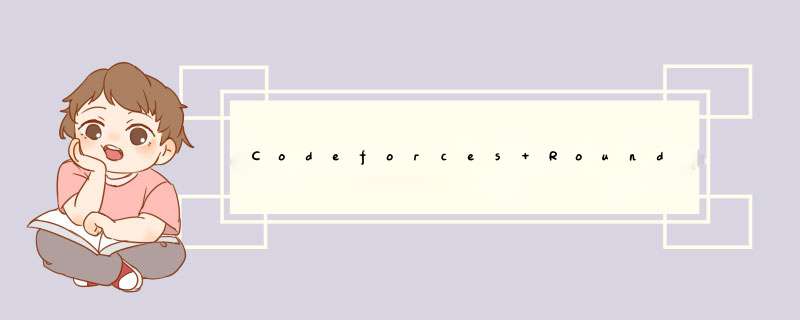
由题 (xb)^a=y
若a=1 则xb=y
即y%x=0时 b=y/x
故y%x=0时 a=1 b=y/x满足题意解
否则 (x*b)^a=y无解 输出 0 0即可
a b输出顺序反啦 WA一发
#include
#define int long long
using namespace std;
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
int x,y;
cin>>x>>y;
if(!(y%x)){
cout<<1<<" "< #include
#define int long long
using namespace std;
int check(string s){
if(s[0]-'a'>0){
if(s[1] >= s[0])
return s[0]-'a';
else{
return s[0]-'a'-1;
}
}
else{
return 0;
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
string s;
cin>>s;
cout<<(s[0]-'a')*26+s[1]-'a'-check(s)<<"\n";
}
return 0;
}
若字符串t中无’a’ 字符串s任意位置可选择交换或不交换 有2^字符串s长度 故返回2^字符串s长度
若字符串t中仅含’a’ 仅有原字符 返回1
若字符串t中不仅仅含’a’ 可无限迭代 返回-1
字符串s任意位置可选择交换或不交换 有2^字符串s长度 故返回2^字符串s长度判错 WA一发
#include
#define int long long
using namespace std;
int solve(string s, string t){
bool flag = false;
for(int i=0;i>t;
while(t--){
string s, s1;
cin>>s>>s1;
cout< 我们可以发现题目里给出的两个 *** 作基本上就是就是一对互逆的 *** 作,我们 *** 作的空间实际上只有在有两个中间位置的时候可以选择一个数放进去或者取出来,模拟几次我们可以发现这种 *** 作只能其实改变一对相邻的数的顺序,所以我们只需要判断从后往前一对对相邻的数字调整后能否让整个数组有序即可.
代码实现#include
#include
#include
using namespace std;
typedef long long LL;
const int maxn = 2e5 + 5, INF = 0x3f3f3f3f;
int a[maxn];
int main(){
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int T;
cin >> T;
while(T--){
int n;
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = n; i > 1; i -= 2)
if (a[i] < a[i - 1])
swap(a[i], a[i - 1]);
cout << (is_sorted(a + 1, a + n + 1) ? "YES" : "NO") << '\n';
}
}
看样例直接猜测 然后WA两发
#include
#define int long long
using namespace std;
int a[200005];
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
int n;
cin>>n;
if(n==1||n==2){
cout<<"YES"<<"\n";
}else{
int mx=0,mn=1000005,mxi=0,mni=0;
for(int i=0;i>a[i];
if(a[i]>mx){
mx=a[i];
mxi=i;
}
if(a[i] *** 作的方法只有三种可能.
1选择整个序列中最小的两个元素,对这两个元素不断减去2,分别把对应位置的值除以2向上取整后相加即可.
2选择相邻的两项,如果其中一项大于另一项的2倍,那么最佳方法就是只在大的那一项上 *** 作减2,答案就是大的那项除以除以2向上取整.如果其中一项并没有大于另一项的2倍,那么 *** 作数就是两项的和除以3向上取整.
3选择中间差一格的两项,先 *** 作他们中间的格子让小的减到0,然后用减2 *** 作大的那项剩下的值.
哎 D题都不会
#include
#include
using namespace std;
typedef long long LL;
const int maxn = 2e5 + 5, INF = 0x3f3f3f3f;
int a[maxn];
int main(){
int n;
scanf("%d", &n);
int minv1 = INF, minv2 = INF;
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
if (a[i] <= minv1) minv2 = minv1, minv1 = a[i];
else if (a[i] < minv2) minv2 = a[i];
}
int res = (minv1 + 1 >> 1) + (minv2 + 1 >> 1);
for(int i = 1; i + 2 <= n; i++)
res = min(res, min(a[i], a[i + 2]) + (abs(a[i] - a[i + 2]) + 1 >> 1));
for(int i = 1; i + 1 <= n; i++){
int t1 = a[i], t2 = a[i + 1];
if (t1 > t2) swap(t1, t2);
if (t2 > 2 * t1) res = min(res, t2 + 1 >> 1);
else res = min(res, (a[i] + a[i + 1] + 2) / 3);
}
cout << res << '\n';
}
每次 *** 作后我们能够知道平面上有多少个点,然后我们也可以很容算出最终这些点都会排在哪些区域,很显然已经在最终的区域的里的点不再需要移动,而不在区域里的点需要移动一次,最终的区域我们一定可以将其划分成两个矩形,所以其实问题就变成了动态求两个矩形内有多少个点.
所以这是一个标准的动态求二维前缀和问题,可以用二维线段树/树状数组或者其他数据结构解决.
哎 D题都不会
#include
#include
using namespace std;
typedef long long LL;
const int maxn = 1005, INF = 0x3f3f3f3f;
char g[maxn][maxn];
int tr[maxn][maxn];
int n, m, q;
inline int lowbit(int x){
return x & -x;
}
void modify(int x, int y, int v){
for(int i = x; i <= n; i += lowbit(i))
for(int j = y; j <= m; j += lowbit(j))
tr[i][j] += v;
}
int query(int x, int y){
int res = 0;
for(int i = x; i; i -= lowbit(i))
for(int j = y; j; j -= lowbit(j))
res += tr[i][j];
return res;
}
int query(int x0, int y0, int x1, int y1){
return query(x1, y1) - query(x1, y0 - 1) - query(x0 - 1, y1) + query(x0 - 1, y0 - 1);
}
int main(){
scanf("%d%d%d", &n, &m, &q);
int sum = 0;
for(int i = 1; i <= n; i++){
scanf("%s", g[i] + 1);
for(int j = 1; j <= m; j++)
if (g[i][j] == '*'){
sum++;
modify(i, j, 1);
}
}
while(q--){
int x, y;
scanf("%d%d", &x, &y);
if (g[x][y] == '*'){
g[x][y] = '.';
sum--;
modify(x, y, -1);
}
else{
g[x][y] = '*';
sum++;
modify(x, y, 1);
}
int t = 0;
if (sum / n) t += query(1, 1, n, sum / n);
if (sum % n) t += query(1, sum / n + 1, sum % n, sum / n + 1);
printf("%d\n", sum - t);
}
}
cute的条件其实就是表示u到v是一条链.所以问题就是一次 *** 作后图上最长的链有多长,而且这个图又是有向无环图(DAG),可以用动态规划更新答案,更新答案的条件就是边起点的出度要大于等于2,边终点的入度也要大于等于2,否则这条边一定会被删掉.
哎 D题都不会
#include
#include
#include
using namespace std;
typedef long long LL;
const int maxn = 2e5 + 5, INF = 0x3f3f3f3f;
int h[maxn], e[maxn], ne[maxn], idx;
int din[maxn], dout[maxn], d[maxn];
int q[maxn], f[maxn];
int n, m;
void topsort(){
int hh = 0, tt = -1;
for(int i = 1; i <= n; i++){
if (!d[i])
q[++tt] = i;
}
while(hh <= tt){
int t = q[hh++];
for(int i = h[t]; ~i; i = ne[i]){
int j = e[i];
if (dout[t] >= 2 && din[j] >= 2) f[j] = max(f[j], f[t] + 1);
if (--d[j] == 0)
q[++tt] = j;
}
}
}
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
din[b]++, d[b]++, dout[a]++;
}
int main(){
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
while(m--){
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
}
fill(f + 1, f + n + 1, 1);
topsort();
cout << *max_element(f + 1, f + n + 1) << '\n';
}
原创不易 转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)