Codeforces Round #786

Codeforces Round #786 (Div. 3) A ~ G 全题解 A. Number Transformation 题意

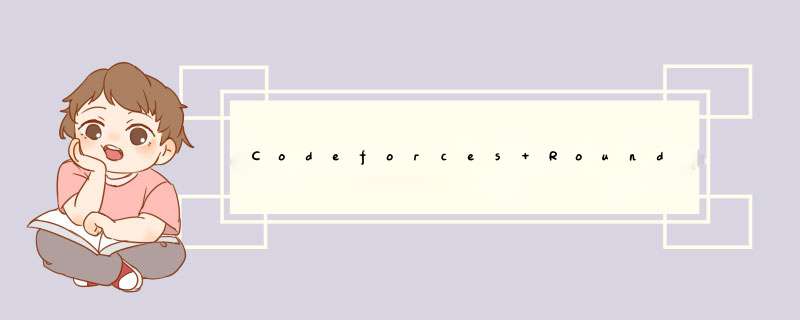
给你两个整数x，y，你需要选择两个正整数a，b使得x乘a次b后等于y，输出a和b
若无解输出0 0

思路

判断是否有解，只需要看y是不是x的倍数，如果不是则无论怎么乘都不能把x变成y
如果有解，我们选一个特殊解 令a为1，b为y/x即可

AC代码

#include
using namespace std;
const int N = 1e6+7;
typedef long long ll;
int main(){
	int T;
	cin>>T;
	while(T--){
		ll a,b;
		cin>>a>>b;
		if(b%a!=0) cout<<"0 0\n";
		else{
			ll k = b/a;
			cout<<"1 "<<k<<endl;
		}
	}
	return 0;
}

B. Dictionary 题意

给你一个两个字符组成的字符串，第一个字符与第二个不同，若a字符串小于字符串，要满足a第一个字符小于b第一个字符或者a第一个字符等于b第一个字符且a第二个字符小于b第二个字符，基于这个规则形成一本字典
Word 1: ab
Word 2: ac
…
Word 25: az
Word 26: ba
Word 27: bc
…
Word 649: zx
Word 650: zy
给出一个字符串,给出字符串在字典的位置

思路

两层for预处理所有字符串的位置

AC代码

#include
using namespace std;
const int N = 1e6+7;
typedef long long ll;
map<string ,int> M;
int main(){
	int T;
	cin>>T;
	int cnt = 1;
	for(char i = 'a';i<='z';i++){
		for(char j = 'a';j<='z';j++){
			string s ="";
			s +=i;
			s +=j;
			if(i==j) continue;
			M[s] = cnt++;
		}
	}
	while(T--){
		string s;
		cin>>s;
		cout<<M[s]<<endl;
	}
	return 0;
}

C. Infinite Replacement 题意

给你两个字符串 t ，k，对于字符串t中的所有字符a来说，都可以变成k，可以变换任意次，问你变换后可以形成多少个不同的字符串， 如果形成无限的字符串输出-1

思路

考虑无限字符串，当 k 里面包含a而且长度大于1时，t 可以无限延长，输出-1
其他情况对于字符串k每个字符a都有变成k或者不变的选择 ， 设k中a字符个数为cnt，那么答案就是2的cnt次方
最后特判一下k为“a” 情况，无论怎么变，答案只能为1

AC思路

#include
using namespace std;
const int N = 1e6+7;
typedef long long ll;
map<string ,int> M;
int main(){
	int T;
	cin>>T;
	while(T--){
		string s,t;
		cin>>s>>t;
		if(t=="a") cout<<"1\n";
		else {
			int cnt = 0;
			for(int i : t){
				cnt += (i=='a');
			}
			int n = s.length();
			if(cnt>=1&&t.length()>1) cout<<"-1\n" ;
			else {
				cnt = 0;
				for(char j : s) if(j=='a') cnt++;
				cout<<(1ll<<cnt)<<endl;
			}
		}
		
	}
	return 0;
}

D - A-B-C Sort 题意

给你一个数组，有两个空数组A，B，对数组进行 *** 作
1 把数组最后一个元素放在A中间，如果A元素是奇数，那么放在中间靠左和靠右都可以
2 把A的中间一个元素，当A有偶数个元素，那么选中间靠左边和右边都可以， 然后放在B数组的最后
问进行完这样的 *** 作后，数组B里面的元素是否是非递减的

思路

可以发现 从最后一个放到中间，在从中间放到最后，可以改变顺序的是相邻两个元素，因为对于每两个元素，放在左右是都可以的，那么做法就是从后往前每次遍历两个元素，逆序则交换位置，最后判断是否非递减

AC代码

#include
using namespace std;
const int N = 1e6+7;
typedef long long ll;
int A[N];
int main(){
	int T;
	cin>>T;
	while(T--){
		int n;
		cin>>n;
		for(int i = 0;i<n;i++){
			cin>>A[i];
		}
		for(int i = n-1;i>=0;i-=2){
			if(A[i-1]>A[i]) swap(A[i],A[i-1]);
		}
		int ok = 1;
		for(int i = 0;i<n-1;i++){
			if(A[i]>A[i+1]) ok = 0;
		}
		if(ok) cout<<"YES\n";
		else cout<<"NO\n";
	}
	return 0;
}

E. Breaking the Wall 题意

你需要破坏至少两个城墙，城墙都是连续的，你可以对任意一个城墙发起进攻，使城墙的血量减少2
而且让左边和右边的城墙减少 1 ，城墙的血量0以下就会被摧毁，问你至少多少次攻击能破坏两个城墙

思路

贪心
1如果破坏的两座城墙没有任何关联，那么答案就是血量最少的两个城墙之和除2
2如果破坏的两座城墙相隔1，那么枚举中间点，计算最少次数让两边的墙破坏,如果两边不都是奇数，那答案是 *** 作3，否则，可以先对中间攻击一次，使两边变成偶数，再用 *** 作3
3如果破坏的两座城墙相临，设两个城墙血量为a，b，（a>b），那么先判断只用破环一个墙就能用aoe破环完隔壁的墙，即 a>2*b时，答案是a/2 ,否则答案为（a+b）/3，证明如下
x，y分别为攻击第一二个城墙的次数 2x + y >= a , x + 2y >= b -> 3x + 3y >= a + b -> x+y >=(a+b)/3

AC代码

#include
using namespace std;
typedef long long ll;
ll a[200009],b[200009],mod=1e9+7,we[5];
map<string,int>has;
int main(){
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	ll i,n,t,ans,x,y,j,m,k,l,r;
	string s,s1;
	j=1;
	cin>>n;
	for(i=1;i<=n;i++){
		cin>>a[i];
		b[i]=a[i];
	}
	sort(b+1,b+1+n);
	ans=(b[1]+1)/2+(b[2]+1)/2;
	for(i=1;i<=n;i++){
		if(i>1){
			x=max(a[i],a[i-1]);
			y=min(a[i],a[i-1]);
			if(y*2>=x){
			k=x-y;
			x-=k*2;
			k+=(x/3*2+x%3);
			}
			else k=(x+1)/2;
			ans=min(ans,k);
		}
		if(i<n){
			x=max(a[i],a[i+1]);
			y=min(a[i],a[i+1]);
			if(y*2>=x){
			k=x-y;
			x-=k*2;
			k+=(x/3*2+x%3);
			}
			else k=(x+1)/2;
			ans=min(ans,k);
		}
		if(i>1&&i<n){
			x=max(a[i-1],a[i+1]);
			y=min(a[i-1],a[i+1]);
			k=y;
			x-=k;
			k+=(x+1)/2;
			ans=min(ans,k);
		}
	}
	cout<<ans;
	return 0;
}

F. Desktop Rearrangement 题意

整理桌面，给你包含’.‘,’*'的图案，分别代表空格和图案，给你q次 *** 作，每次 *** 作令某一个位置空格变成图案或者图案变成空格，你可以移动图案到任意位置，问你每次 *** 作后需要移动最少次数使桌面整理好（好的定义就是window桌面的图标顺序）

思路

我们先判断哪些位置应该处理好的，如果说图案的位置在应该处理好的位置内，那么不需要整理，否则需要整理
有个细节 ，修改位置刚好处在应该处理好的位置时要额外判断

#include
using namespace std;
const int N = 1e6+7;
typedef long long ll;
char A[2000][2000];
int n,m,k;
void add(int &x,int &y){
	x++;
	if(x>n) x = 1,y++;
}
void mius(int &x,int &y){
	x--;
	if(x<=0) x = n,y--;
}
// 1 2
int to_pos(int x,int y){
	return (y-1)*n+x;
}
int main(){
	int cnt = 0,need = 0;
	cin>>n>>m>>k;
	for(int i = 1;i<=n;i++){
		for(int j = 1;j<=m;j++){
			cin>>A[i][j];
			if(A[i][j]=='*') cnt++;
		}
	}
	int t_cnt = 0;
	int i,j;
	for( i = 1;i<=m;i++){
		for( j = 1;j<=n;j++){
			t_cnt++;
			if(t_cnt>cnt) break;
			if(A[j][i]=='.') need++;
		}
	}
	int nx = cnt%n,ny = cnt/n+1;
	if(cnt%n==0) ny--,nx = n;
	while(k--){
		int x,y;cin>>x>>y;
		if(A[x][y]=='.') {
			cnt++; //图标增加1 
			if(cnt<to_pos(x,y)) need++;
			add(nx,ny);
			if((nx!=x||ny!=y)&&A[nx][ny]=='*') need--;
			A[x][y] = '*';
		}
		else {
			cnt--; //图标减少1 
			if(cnt<to_pos(x,y))need--;
			if(A[nx][ny]=='*') need++;
			mius(nx,ny);
			A[x][y] = '.';
		}
		cout<<need<<"\n";
	
	}
	return 0;
}

G - Remove Directed Edges 题意

给你一个有向图，你可以删除边，要求最后的图中每个点的入度和出度都要减少，或者保持0
问你图中最大点集大小，里面任意两点可以单向到达u->v或者v->u

思路

最后的点集中，只有一条最长链串在一起，那么我们需要得到这个图中最长路即可，但是由于要求最后的图中每个点的入度和出度都要减少，或者保持0，所有在遍历的时候要求入度和出度都要大于1才能往下搜，否则遍历的这条边一定会被删除

AC代码

#include
using namespace std;
const int N = 2e5+7;
typedef long long ll;
vector<int> v[N];
int in[N],out[N],dp[N],ans = 0;
void dfs(int u){
	if(dp[u]) return ;
	dp[u] = 1;
	if(out[u]<2) return;
	for(int i : v[u]){
		dfs(i);
		if(in[i]>=2) 
		dp[u] = max(dp[i] + 1,dp[u]); 
	}
}
int main(){
	int n,m;
	cin>>n>>m;
	for(int i = 0;i<m;i++) {
		int a,b;
		cin>>a>>b;
		v[a].push_back(b);
		in[b]++,out[a]++;
	}
	for(int i = 1;i<=n;i++){
		dfs(i);
	}
	for(int i = 1;i<=n;i++){
		ans = max(ans,dp[i]);
	}
	cout<<ans<<endl;
	return 0;
}

总结一下，城墙那题被hack的好惨，没有考虑到相隔1的时候，G题赛后也没有不补出来，感觉无从下手，没有想到考虑最后点集的特性，它由一条链形成