GCN的简单理解

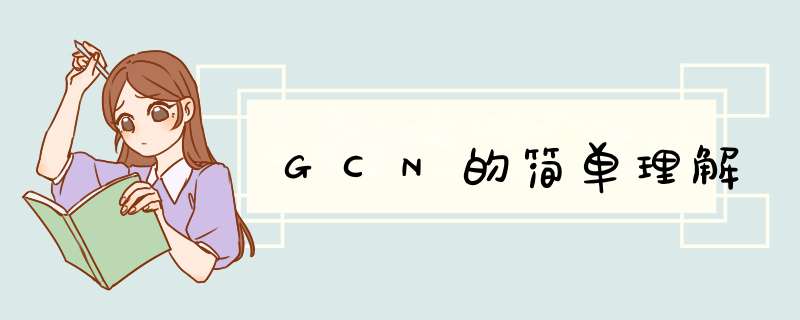
流程图解
pytorch实现
公式推导

H l = G C N ( H l − 1 ; A ) = σ ( A ~ H l − 1 W l + B l ) H^{l} = GCN(H^{l-1} ;A)=\sigma( \tilde A H^{l-1}W^{l}+B^{l}) Hl=GCN(Hl−1;A)=σ(A~Hl−1Wl+Bl)
A ~ \tilde A A~为邻接矩阵， H为上一层输出， W为可训练权重， B为偏置
即
( 1 )          x ∗ G g θ = θ ( D ~ − 1 2 A ~ D ~ − 1 2 ) x (1) \ \ \ \ \ \ \ \ x*Gg_{\theta} = \theta(\tilde D^{-{1\over2}} \tilde A \tilde D^{-{1\over2}})x (1)        x∗Ggθ​=θ(D~−21​A~D~−21​)x
D ~ \tilde D D~为度矩阵
还等于
( 2 )          x ∗ G g θ = θ ( D ~ − 1 A ~ ) x (2) \ \ \ \ \ \ \ \ x*Gg_{\theta} = \theta(\tilde D^{-1} \tilde A )x (2)        x∗Ggθ​=θ(D~−1A~)x
进一步拆解(1)
D ~ − 1 2 A ~ D ~ − 1 2 X = ( D + I ) − 1 2 ( A + I ) ( D + I ) − 1 2 X \tilde D^{-{1\over 2}} \tilde A \tilde D^{-{1\over 2}} X = (D + I)^{-{1\over 2}}(A+I)(D + I)^{-{1\over 2}}X D~−21​A~D~−21​X=(D+I)−21​(A+I)(D+I)−21​X
进一步拆解(2)
D ~ − 1 A ~ X = ( D + I ) − 1 ( A + I ) X \tilde D^{-1} \tilde A X = (D + I)^{-1}(A+I)X D~−1A~X=(D+I)−1(A+I)X
I为单位矩阵，表示添加自身节点链接