C语言实现Hilbert函数。要求可阶数可输入，结果与以下matlab程序一致

function [x,y] = hilbert(n)

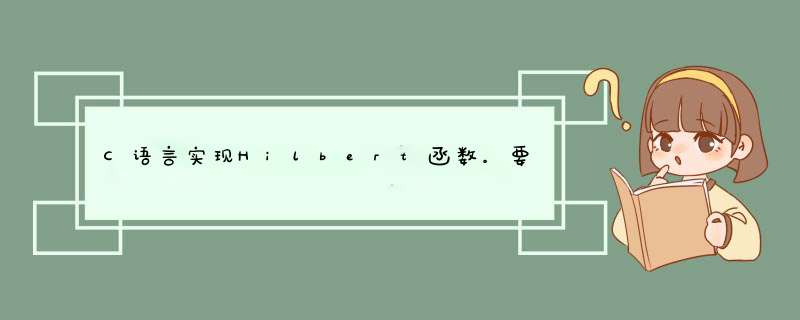
if n<=0

  x=0

  y=0

else

  [xo,yo]=hilbert(n-1)

  x=.5*[-.5+yo -.5+xo .5+xo  .5-yo]

  y=.5*[-.5+xo  .5+yo .5+yo -.5-xo]

end

希尔伯特矩阵（Hilbert matrix）是一种数学变换矩阵，正定，且高度病态（即，任何一个元素发生一点变动，整个矩阵的值和逆矩阵都会发生巨大变化），病态程度和阶数相关。在线性代数中，希尔伯特矩阵是一种系数都是单位分数的方块矩阵。

方法/步骤

数学形式

Hilbert矩阵是一种著名的“坏条件”矩阵。该矩阵的元素的数学表达式是a(i,j)=1/(i+j-1)。下面就展示一下五阶的Hilbert矩阵的数学表示形式。

用for循环生成Hilbert矩阵

下面我们就根据数学表达式，借助for循环生成Hilbert矩阵，具体的运算代码和结果如下图所示，为了和第一步中数学表示形式的Hilbert矩阵做比较，本次计算也选择5阶。

矩阵空间预配置可提高运行速度

在对矩阵的运算中，对矩阵空间进行预配置可以提高运行速度，尤其对高阶矩阵的运算速度影响明显。我们可以通过计时函数tic和toc进行验证。tic表示计时开始，toc表示计时结束。图一为不进行矩阵空间预配置所用时间，为3.2464秒；图二是进行矩阵空间预配置时计算所用时间，为0.072233。可以很明显看出提高了运行速度。

向量化编程产生Hilbert矩阵

当我们采用向量化编程产生Hilbert矩阵时，可以大大提高运行速度，所以在平时编程时应尽量采用向量化编程，但须对matlab有较高的认知。如图所示所用时间为0.031616秒，所用时间比前两种都短。

用matlab自带函数eig计算

这里我们用matlab自带的产生Hilbert矩阵的函数hilb(n)计算一下。所用的时间为0.003173秒。可以看出所用的时间最短，所以在编程时我们应该尽量使用matlab已经有的相应功能的函数，如实在找不到在自己变。这样可以节省计算时间。

希尔伯特矩阵的逆

此外matlab还自带有求希尔伯特矩阵的逆的函数invhilb(n)，其功能是求n阶的希尔伯特矩阵的逆矩阵。我们看一下，具体代码和结果如下图。有图可以看出用时还是比较短的。

END

注意事项

本经验中计算所用的时间受电脑配置、matlab版本、该程序是否首次运行等因素影响，其结果会有所变化。

#define PI 3.1415926

#define PI2 6.2831853

#include "stdio.h"

#include "math.h"

/* inv=1 forward transforminv=-1 inverse transform */

fft(float sr[],float sx[],int m0,int inv)

{

int i,j,lm,li,k,lmx,np,lix,mm2

float t1,t2,c,s,cv,st,ct

if(m0<0)

return

inv=-inv

lmx=1

for(i=1i<=m0++i)

lmx+=lmx //get 2**m0

cv=PI2/(double)lmx

ct=cos(cv)st=sin(cv)*inv

np=lmxmm2=m0-2

/* fft butterfly numeration */

for(i=1i<=mm2++i)

{

lix=lmxlmx/=2

c=cts=st

for(li=0li<npli+=lix)

{

j=lik=j+lmx

t1=sr[j]-sr[k]t2=sx[j]-sx[k]

sr[j]+=sr[k]sx[j]+=sx[k]sr[k]=t1sx[k]=t2

++j++k

t1=sr[j]-sr[k]t2=sx[j]-sx[k]

sr[j]+=sr[k]sx[j]+=sx[k]

sr[k]=c*t1-s*t2sx[k]=s*t1+c*t2

}

for(lm=2lm<lmx++lm)

{

cv=cc=ct*c-st*ss=st*cv+ct*s

for(li=0li<npli+=lix)

{

j=li+lmk=lmx+j

t1=sr[j]-sr[k]t2=sx[j]-sx[k]

sr[j]+=sr[k]sx[j]+=sx[k]

sr[k]=c*t1-s*t2sx[k]=s*t1+c*t2

}

}

cv=ctct=2.0*ct*ct-1.0st=2.0*st*cv

}

/* 4 points DFT */

if(m0>=2)

for(li=0li<npli+=4)

{

j=lik=j+2

t1=sr[j]-sr[k]t2=sx[j]-sx[k]

sr[j]+=sr[k]

sx[j]+=sx[k]

sr[k]=t1sx[k]=t2

++j++k

t1=sr[j]-sr[k]t2=sx[j]-sx[k]

sr[j]+=sr[k]sx[j]+=sx[k]

sr[k]=-inv*t2sx[k]=inv*t1

}

/* 2 points DFT */

for(li=0li<npli+=2)

{

j=lik=j+1

t1=sr[j]-sr[k]t2=sx[j]-sx[k]

sr[j]+=sr[k]sx[j]+=sx[k]

sr[k]=t1sx[k]=t2

}

/* sort according to bit reversal */

lmx=np/2j=0

for(i=1i<np-1++i)

{

k=lmx

while(k<=j)

{

j-=kk/=2

}

j+=k

if(i<j)

{

t1=sr[j]sr[j]=sr[i]sr[i]=t1

t1=sx[j]sx[j]=sx[i]sx[i]=t1

}

}

/* if Inverse FFT, multiply 1.0/np */

if(inv!=1.0)

return

t1=1.0/np

for(i=0i<np++i)

{

sr[i]*=t1sx[i]*=t1

}

}

main()

{

float xr[2048],xi[2048],xt[2048]

int i,np,nfft,k,nf

float t,dt,df,f,hf

float f0=10,f1=20,f2=30

FILE *fp1,*fp2

char fil1[60],fil2[60]

printf("ENTER TIME SIGNAL FILE\n")

scanf("%s",fil1)

printf("ENTER AMPLITUDE SPECTRUM FILE\n")

scanf("%s",fil2)

printf("SAMPLE POINTS?\n")

scanf("%d",&np)

printf("SAMPLE INTERVAL(S)?\n")

scanf("%f",&dt)

printf("HIGH CUTOFF FREQUENCY(Hz)?\n")

scanf("%f",&hf)

fp1=fopen(fil1,"w")

fp2=fopen(fil2,"w")

for(i=0i<npi++)

{ t=(i-np/2)*dt

if(t!=0.0)xt[i]=1.0/(PI*t)

else xt[i]=0.0

xr[i]=xt[i]

}

// calculate fft point

k=log(np*1.0)/log(2.0)

if(np>pow(2.0,k*1.0))k=k+1

nfft=pow(2.0,k*1.0)

df=1.0/(nfft*dt)

nf=hf/df+1

printf("nfft=%d k=%d\n",nfft,k)

printf("dt=%f df=%f nf=%d\n",dt,df,nf)

// fill zero

if(np<nfft)

{for(i=npi<nffti++)

xr[i]=0

}

for(i=0i<nffti++)

xi[i]=0.0

// calculate fft

fft(xr,xi,k,1)

// output amplitude and argument

for(i=0i<nfi++)

{ f=i*df

fprintf(fp2,"%d %8.2f %12.4f %12.4f\n",i,f,atan(xr[i]/xi[i]),sqrt(xr[i]*xr[i]+xi[i]*xi[i]))

}

fft(xr,xi,k,-1)

for(i=0i<npi++)

{ t=i*dt

fprintf(fp1,"%10d %10.4f %10.4f %10.4f\n",i+1,t,xt[i],xr[i])

}

fclose(fp1)

fclose(fp2)

}

---