一道matlab编程题

1.

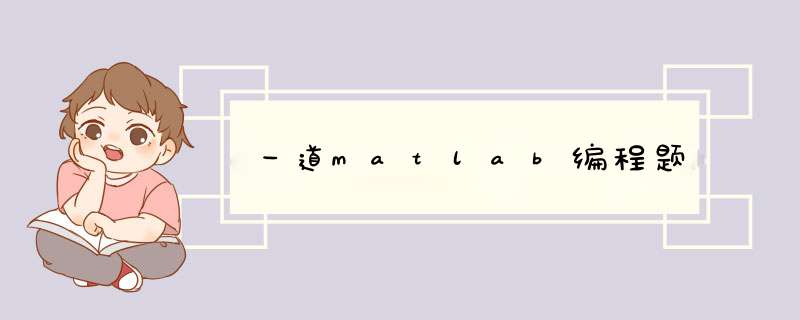
首先举一个简单的例子：求y=x^2

，在x为[0,2]上的曲线长度。

%%把下面的复制粘贴进MATLAB

syms

t

x=t

y=t^2

df=@(t)(1+4*t.^2).^0.5

%%MATLAB早期版本不支持@功能

quad(df,0,1)

%%%

答案ans=1.4789

2.

再回答你的问题：

clc

clear

syms

t

x=sin

(t)

y=t^2

z=log(t+1)

%%%

dL=

sqrt((diff(x)^2+diff(y)^2+diff(z)^2))

求曲线长度公式

%%%

dL=(1/(t

+

1)^2

+

cos(t)^2

+

4*t^2)^(1/2)

即上述公式的数学表达式

df=

@(t)(1./(t

+

1).^2

+

cos(t).^2

+

4*t.^2).^(1/2)

%%

将上述表达式卸载@(t)之后，注意加'.'运算。

quad(df,0,20)

%%%

答案

ans=400.9527

楼主你好！

不知我的答案你是否满意：

（1）做波形显示以及fft变换，程序如下:

[y,fs]=wavread('E:\MATLAB6p5\work\3.wav')%读出信号，采样率。

y=y(:,1)%取单声道。

sigLength=length(y)

Y = fft(y,sigLength)

Pyy = Y.* conj(Y) / sigLength

halflength=floor(sigLength/2)

f=Fs*(0:halflength)/sigLength

figureplot(f,Pyy(1:halflength+1))xlabel('Frequency(Hz)')%画频域波形

t=(0:sigLength-1)/Fs

figureplot(t,y)xlabel('Time(s)')%画时域波形

(2)关于滤波

声音频率主要集中在0~1KHZ，我想虑掉500hz以下的频率，因此采用一个高通滤波器

这里我使用了一个10阶butterworth高通滤波器，边带是500hz，但是这不能直接用，因为声音文件的采样率是44k，500hz相对于44k来说太小了。所以我得先把我的声音欠采样，然后再滤波。程序如下:

[k,Fs,bits]=wavread('E:\MATLAB6p5\work\3.wav')

k=k(:,1)

y_temp=k(1:90000)

dfactor=3

y=decimate(y_temp,dfactor)

[b,a] = butter(10,500/(Fs/(dfactor*2)),'high')

y=filter(b,a,y)

y=interp(y,dfactor)

sigLength=length(y)

Y = fft(y,sigLength)

Pyy = Y.* conj(Y) / sigLength

halflength=floor(sigLength/2)

f=Fs*(0:halflength)/sigLength

figureplot(f,Pyy(1:halflength+1))xlabel('Frequency(Hz)')%滤波后的频域波形

t=(0:sigLength-1)/Fs

figureplot(t,y,t,y_temp)xlabel('Time(s)')%滤波后的时域波形

wavwrite(y,Fs,'3_')%保存处理后的声音文件，文件名为”3_”.

（3）

Matlab代码示例：

clear

Fs=1000%采样频率

n=0:1/Fs:1

%产生含有噪声的序列

xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n))

window=boxcar(length(xn))%矩形窗

nfft=1024

[Pxx,f]=periodogram(xn,window,nfft,Fs)%直接法

plot(f,10*log10(Pxx))

间接法：

间接法先由序列x(n)估计出自相关函数R(n)，然后对R(n)进行傅立叶变换，便得到x(n)的功率谱估计。

Matlab代码示例：

clear

Fs=1000%采样频率

n=0:1/Fs:1

%产生含有噪声的序列

xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n))

nfft=1024

cxn=xcorr(xn,'unbiased')%计算序列的自相关函数

CXk=fft(cxn,nfft)

Pxx=abs(CXk)

index=0:round(nfft/2-1)

k=index*Fs/nfft

plot_Pxx=10*log10(Pxx(index+1))

plot(k,plot_Pxx)

改进的直接法：

对于直接法的功率谱估计，当数据长度N太大时，谱曲线起伏加剧，若N太小，谱的分辨率又不好，因此需要改进。

1. Bartlett法

Bartlett平均周期图的方法是将N点的有限长序列x(n)分段求周期图再平均。

Matlab代码示例：

clear

Fs=1000

n=0:1/Fs:1

xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n))

nfft=1024

window=boxcar(length(n))%矩形窗

noverlap=0%数据无重叠

p=0.9%置信概率

[Pxx,Pxxc]=psd(xn,nfft,Fs,window,noverlap,p)

index=0:round(nfft/2-1)

k=index*Fs/nfft

plot_Pxx=10*log10(Pxx(index+1))

plot_Pxxc=10*log10(Pxxc(index+1))

figure(1)

plot(k,plot_Pxx)

pause

figure(2)

plot(k,[plot_Pxx plot_Pxx-plot_Pxxc plot_Pxx+plot_Pxxc])

2. Welch法

Welch法对Bartlett法进行了两方面的修正，一是选择适当的窗函数w(n)，并再周期图计算前直接加进去，加窗的优点是无论什么样的窗函数均可使谱估计非负。二是在分段时，可使各段之间有重叠，这样会使方差减小。

Matlab代码示例：

clear

Fs=1000

n=0:1/Fs:1

xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n))

nfft=1024

window=boxcar(100)%矩形窗

window1=hamming(100)%海明窗

window2=blackman(100)%blackman窗

noverlap=20%数据无重叠

range='half'%频率间隔为[0 Fs/2]，只计算一半的频率

[Pxx,f]=pwelch(xn,window,noverlap,nfft,Fs,range)

[Pxx1,f]=pwelch(xn,window1,noverlap,nfft,Fs,range)

[Pxx2,f]=pwelch(xn,window2,noverlap,nfft,Fs,range)

plot_Pxx=10*log10(Pxx)

plot_Pxx1=10*log10(Pxx1)

plot_Pxx2=10*log10(Pxx2)

figure(1)

plot(f,plot_Pxx)

pause

figure(2)

plot(f,plot_Pxx1)

pause

figure(3)

plot(f,plot_Pxx2)

希望我的答案能够帮得到你！

谢谢！

能量有限平均功率为零的信号是能量信号，如单位冲击信号；

能量无限，平均功率有限的信号是功率信号。

题中信号有一个常量10，平均功率不为零且有限，能量无限，属于"功率信号“

功率为：10^2+4^2+2^2=120

---