matlab画相图

参考代码：

function zd1958627691757107380

X0 = [-0.4 0.2

    -0.4 1

    -0.38 1.25

    -0.4 1.6

    0.7 -0.35

    1.6 -0.3

    1.6 0.8

]

clf

hold on

plot([0 0],[-0.4 1.8],'k')

plot([-0.4 1.8],[0 0],'k')

text(-0.1,1.7,'x_1')

text(1.7,-0.1,'x_2')

axis tight

box on

for ii=1:size(X0,1)

    x0 = X0(ii,:)

    [t,x] = ode45(@f,[0 20],x0)

    庆链悄plot(x(:,1),x(:,2),'k','linewidth',2)

    drawnow

end

function dx = f(t,x)

dx = [0.5*(-h(x(1))+x(2)) 0.2*(-x(1)-1.5*x(2)+1.2)]

function 誉渣y = h(x)

y = 17.76*x - 103.79*x^2 + 229.62*x^3 - 226.31*x^4 + 83.72*x^5

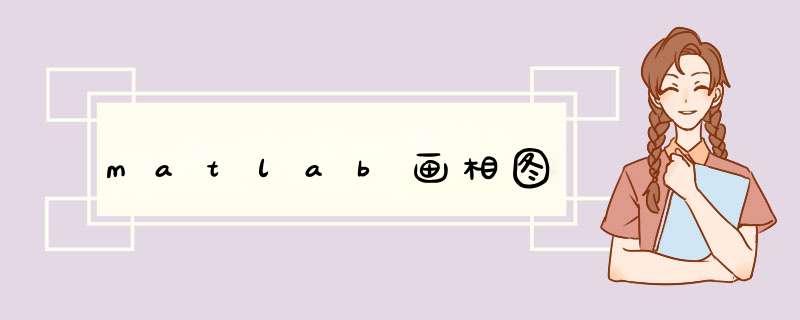
相图大致唤蠢如下：

该非线性系统的终态与初值关系很大，我尝试了很多初值也未能找到经过Q2的曲线。希望楼主能给出该系统的有关理论分析在什么文献上可以查到，我再进一步完善。

相位图是指p（丛衡t）与q（t）之间的变化。如何得到扮厅可以按下列方法来求解。

1、根据给出的厅郑隐微分方程组，自定义一个函数ode_fun，其内容

function dy=ode_fun(t,x)

dy=[x(1)*(1-x(1))*(2-2*x(2))x(2)*(1-x(2))*(0.5-2*x(1))] %p—x(1)、q—x(2)

2、利用ode45（）函数，求解t、p、q 的数值解

3、利用plot（）函数，绘制p（t）与q（t）相位曲线图

4、假定本微分方程组的初始条件，p（0）=0.01；q（0）=0.05

5、按上述方法编程，可得到如下结果。

首先，你提供的问题不完罩档衫整，缺k、β、η1、η2具体数值，还缺S（0）、I（0）的初值条件。

其二，用dsolve（）解出S(t)、I(t)的表达式物腔，蠢吵然后用plot（）绘出S与I的相图

k=？，

beta=? %β

eta1=? %η1

eta2=? %η2

syms S(t) I(t)

DS=diff(S,1)DI=diff(I,1)

[S,I]=dsolve(DS==k-beta*S*I-eta1*S,DI==beta*S*I-eta2*I,S(0)==?,I(0)==?)

t=0:n

S=eval(S)I=eval(I)

plot(S,I)  %相平面图

---