446X25一25x46简便计算怎么做?

简便计算
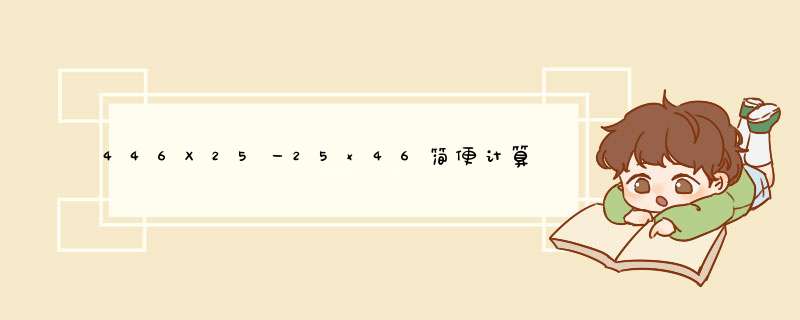
简便计算是一种特殊的计算，它运用了运算定律与数字的基本性质，从而使计算简便，使一个很复杂的式子变得很容易计算出得数。
1、分组凑整法:
直接根据运算定律和性质，把算式中能奏成整十、整百、整千-的数先计算,使计算筒便。
例如:(1)218+17+82=(218+82)+17=300+17=317。
2、补数计算法:
対接近整百、整千的数，可以补上一个数，使它成内整百、整千的数，使计算筒便
例如:4616-998=4616-(1000-2)=4616-1000+2=3616+2=3618。
3、基准数计算法:
求一些大小不等而又比较接近的几个数之和，可以从中选定一个数作为基准数，然后把各个数与基准数的差，累计起来，再加上基准数与项数之积。
如:38+41+37+43+45+39+44+42=(40-2)+(40+1)+(40-3)+(40+3)+(40+5)+(40-1)+(40+4)+(40+2)=40X8+(1+3+5+4+2-2-3-1=320+9=329。
最终答案是10000

96+97+95+83+90+89+92的基准数用90等于96=90+6 97=90+7 95=90+5
83=90-7 90=90 89=90-1 92=90+2
90X7+6+7+5-7-1+2=630+6+7+5-7-1+2=642

=71×（124-1）-7×23
=71×123-7×23
=8572
扩展：小学数学简便计算的几种方法
1、分组凑整法:
直接根据运算定律和性质，把算式中能奏成整十、整百、整千-的数先计算,使计算筒便。
例如:(1)218+17+82=(218+82)+17=300+17=317。
2、补数计算法:
対接近整百、整千的数，可以补上一个数，使它成内整百、整千的数，使计算筒便
例如:4616-998=4616-(1000-2)=4616-1000+2=3616+2=3618。
3、基准数计算法:
求一些大小不等而又比较接近的几个数之和，可以从中选定一个数作为基准数，然后把各个数与基准数的差，累计起来，再加上基准数与项数之积。
如:38+41+37+43+45+39+44+42=(40-2)+(40+1)+(40-3)+(40+3)+(40+5)+(40-1)+(40+4)+(40+2)=40X8+(1+3+5+4+2-2-3-1=320+9=329。

八分之七乘以七加八分之三简便计算：

7/8×7+3/8

=0875×7+0375

=6125+0375

=65

将分数化为小数进bai行运算：7/8=0875；3/8=0375。

扩展资料

简便计算方法：

1、基准数法

若干个都接近某数的数相加，可以把某数作为基准数，然后把基准数与相加的个数相乘，再加上各数与基准数的差，就可以得到计算结果。

例如：81+85+82+78+79

=80x5+（1+5+2-2-1）

=400+5

=405

2、拆分法

主要是拆开后的一些分数互相抵消，达到简化运算的目的，一般形如1/ax（a+1）的分数可以拆分成。1/a-1/a+1。

例如：1/1x2+1/2x3+1/3x4+1/4x5+1/5x6

=1_1/2+1/2-1/3+1/3-1/4+1/4-1/5+1/5-1/6

=1-1/6

=5/6

这个题的简便计算方法是采用基准数计算法。
所谓基准数计算法，就是如果在一列数中，各个数都接近某一个数，那么就以这个接近的数为基准，将其它数化为与这个基准数的和或者差，然后用基准数乘以这列数的个数，再加上其他是零头数的计算结果。
58+61+63+59+60+64+57+65
因为这列数都接近60，所以取基准数为60。
58+61+63+59+60+64+57+65
=60×8-2+1+3-1+0+4-3+5
=480+7
=487

---